رياضيات فصل أول

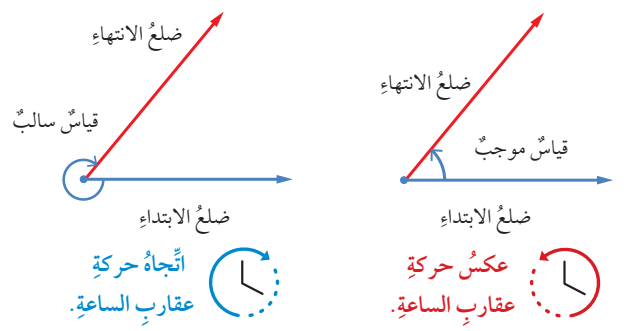
الزاوية هي اتحاد شعاعين لهما نقطة البداية نفسها. والنقطة المشتركة تعرف براس الزاوية، أما الشعاعان فيسمى أحدهما ضلع الابتداء، والآخر ضلع الانتهاء.

يوجد قياسان لاي زاوية، أحدهما موجب عندما يدور ضلع الانتهاء عكس اتجاه حركة عقارب الساعة، والآخر سالب حين يدور ضلع لانتهاء مع اتجاه حركة عقارب الساعة 

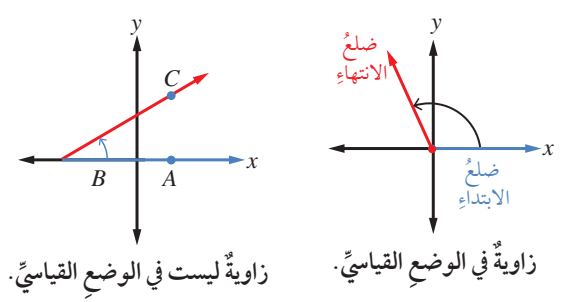
تكون الزاوية المرسومة في المستوى الإحداثي في الوضع القياسي إذا كان رأسها عند نقطة الأصل $\left(0,0\right)$، وضلع ابتدائها منطبقا على محور x الموجب 

مثال 

أحدد إذا كانت الزاويتان الآتيتان في وضع قياسي أم لا، مبينا السبب: 

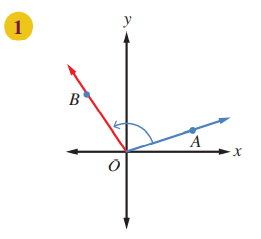
الزاوية AOB ليست في وضع قياسي، لان ضلع ابتدائها لا ينطبق على محور x الموجب 

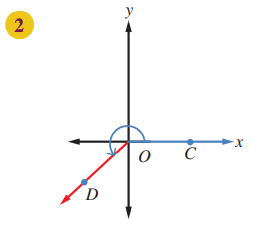
الزاوية COD في وضع قياسي؛ لأن صلع ابتدئها ينطبق على محور x الموجب، وارسها على نقطة الاصل O

اذا دار ضلع انتهاء زاوية في الوضع القياسي دورة كاملة عكس اتجاه حركة عقارب الساعة، فانه يصنع زاويا قياسياتها بين $360° و 0°$. واذ استمر في دورانه، فانه يصنع زوايا قياسياتها اكبر من $360°$

مثال 

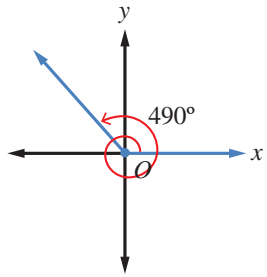
ارسم في الوضع القياسي الزاوية المعطى قياسها في ما ياتي، محددا مكانها: 

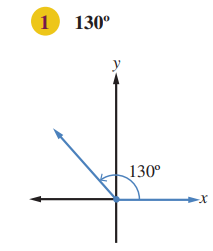
ارسم المحورين الاحداثيين، ومن نقطة الاصل ارسم ضلع الابتداء منطبقا على محور x الموجب، ثم  اضع مركز المنقلة على نقطة الصل، وتدريج المنقلة $0°$ على ضلع الابتداء، ثم اعين نقطة مقابل التدريج $130°$. بعد ذلك ارسم ضلع الانتهاء من نقطة الاصل الى النقطة التي عينتها، فاجد ان ضلع انتهاء الزاوية يقع في الربع الثاني 

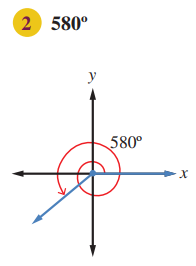
بما ان $580°=360°+220°$، فان ضلع انتهاء الزاوية $580°$ هو نقسه ضلع انتهاء الزاوية $220°$ الذي يقع في الربع الثالث 

---

دائرة الوحدة هي دائرة مركزها نقطة الاصل، وطول نصف قطرها وحدة واحدة.

rاذا رسمت الزاوية $\theta$ في الوضع القياسي، فان ضلع انتهائها يقطع دائرة الوحدة في نقطة وحيدة هي $P\left(x,y\right)$. ومع تغير قياس الزاوية يتغير موقع النقطة P على الدائرة، ويتغير احداثياها 

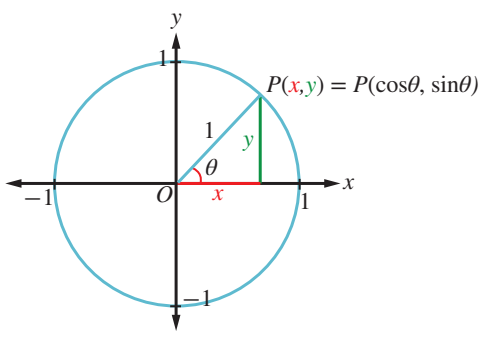
يمكن تعريف النسب المثلثية للزاوية $\theta$ بدلالة احداثيي P كما ياتي: 

$$\begin{gathered} sin \theta =\frac{\mathrm{المقابل} }{\mathrm{الوتر} }=\frac{y}{1}=y \cos \theta =\frac{\mathrm{المجاور} }{\mathrm{الوتر} }=\frac{x}{1}=x \\ \tan \theta =\frac{\mathrm{المقابل} }{\mathrm{المجاور} }=\frac{y}{x},x\ne 0 \end{gathered}$$

مثال 

اجد النسب المثلثية الاساسية للزاوية $\theta$ المرسومة في الوضع القياسي، التي يقطع ضلع انتهائها  دائرة الوحدة في النقطة الواردة في ما ياتي: 

$$\begin{gathered} 1) P\left(-0.6,0.8\right) \\ \sin \theta =y=0.8, \cos \theta =x=-0.6, \tan \theta =\frac{y}{x}=\frac{0.8}{-0.6}=-\frac{4}{3} \\ 2) P\left(\frac{5}{13},-\frac{12}{13}\right) \\ \sin \theta =y=-\frac{12}{13}, \cos \theta =x=\frac{5}{13}, \tan \theta =\frac{y}{x}=\frac{-12l13}{5l13}=-\frac{12}{5} \end{gathered}$$ 

عند رسم الزاوية $\theta$ في الوضع القياسي، قد يقع ضلع انتهائها في احد الارباع الاربعة، فيقال عندئد ان الزاوية $\theta$ واقعة في الربع كذا، وقد ينطبق ضلع انتهائها على احد المحورين الاحداثيين، فتسمى الزاوية $\theta$ في هذه الحالة زاوية ربعية 

مفهوم اساسي 

الزوايا الربعية  في دائرة الوحدة: 

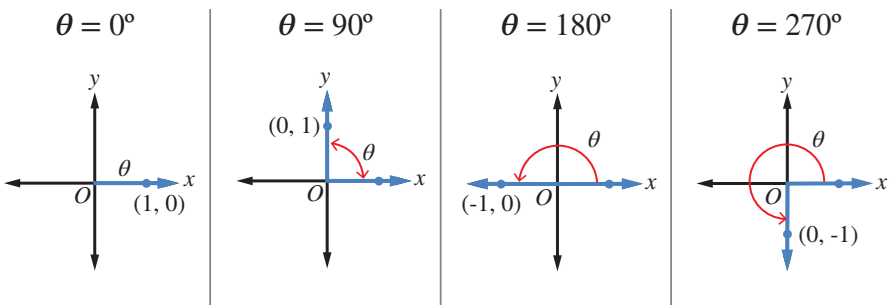
يمكن تحديد النسب المثلثية للزاويا الربعية من احداثيات نقاط تقاطع دائرة الوحدة مع المحورين الاحداثيين. فمثلا، يتقاطع ضلع انتهاء الزاوية $90°$ في الوضع القياسي مع دائرة الوحدة في النقطة $P\left(0,1\right)$. وبذلك، فان: $tan 90°\mathrm{ويكون،} cos 90°=0،sin 90°=1$ غير معرف لانه لا تجوز القسمة على صفر 

مثال 

اين يقطع ضلع انتهاء الزاوية التي قياسيها $180°$ دائرة الوحدة اذا رسمت في الوضع القياسي؟ اجد النسب المثلثية الاساسية لها 

يقطع ضلع انتهاء الزاوية التي قياسها $180°$ دائرة الوحدة في النقطة $C\left(-1,0\right)$، اذن: 

$\sin 180°=y=0, \cos 180°=x=-1, \tan 180°=\frac{y}{x}=\frac{0}{-1}=0$

اذا كانت $\theta$ زاوية حادة، فانه يمكن رسم مثلث قائم الزاوية تكون $\theta$ احدى زواياه 

$$\begin{gathered} {\left(AB\right)}^2+{\left(BC\right)}^2={\left(AC\right)}^2 \\ \frac{{\left(BC\right)}^2}{{\left(AC\right)}^2}+\frac{{\left(AB\right)}^2}{{\left(AC\right)}^2}=\frac{{\left(AC\right)}^2}{{\left(AC\right)}^2} \\ {\left(\frac{BC}{AC}\right)}^2+{\left(\frac{AB}{AC}\right)}^2=1 \\ {\left(\cos \theta \right)}^2+{\left(\sin \theta \right)}^2=1 \end{gathered}$$

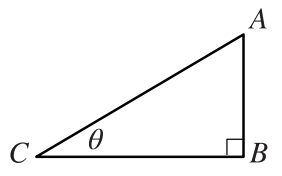
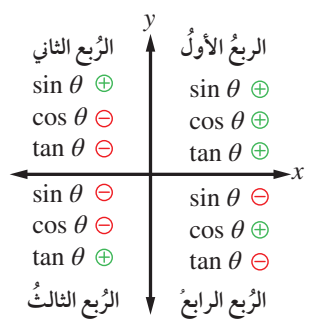
تظل هذه النتيجة صحيحة بقطع النظر عن قياس الزاوية $\theta$، وهي تستعمل لايجاد احدى هاتين النسبتين اذا علمت الاخرى ولكن يجب مراعاة اشارات النسب المثلثية؛ فهي تختلف بحسب الربع الذي يقع فيه ضلع انتهاء الزاوية في الوضع القياسي كما هو موضح في الشكل المجاور 

مثال 

اجد قيمة النسبتين الاساسيتين الباقيتين اذا كان: 

1) $\sin \theta =-\frac{1}{5}$، ووقع ضلع انتهاء $\theta$ في الوضع القياسي في الربع الثالث 

$$\begin{gathered} {\cos }^2 \theta +{\sin }^2 \theta =1 \\ {\cos }^2 \theta +{\left(\frac{-1}{5}\right)}^2=1 \\ {\cos }^2 \theta =1-\frac{1}{25}=\frac{24}{25} \\ \cos \theta =\pm \frac{\sqrt{24}}{5} \\ \cos \theta =-\frac{\sqrt{24}}{5} \\ \tan \theta =\frac{\sin \theta }{\cos \theta }=\frac{-1/5}{-\sqrt{24}/5}=\frac{1}{\sqrt{24}} \end{gathered}$$

2) $\tan \theta =-3.5$، ووقع ضلع انتهاء $\theta$ في الوضع القياسي في الربع الثاني 

$$\begin{gathered} \tan \theta =\frac{\sin \theta }{\cos \theta } \\ \frac{\sin \theta }{\cos \theta }=-3.5 \\ \sin \theta =-3.5 \cos \theta \\ {\cos }^2 \theta + {\sin }^2 \theta =1 \\ {\cos }^2 \theta + {\left(-3.5 \cos \theta \right)}^2=1 \\ {\cos }^2 \theta +12.25 {\cos }^2 \theta =1 \\ 13.25 {\cos }^2 \theta =1 \\ {\cos }^2 \theta =\frac{1}{13.25} \\ \cos \theta =\pm \sqrt{\frac{1}{13.25}}\approx \pm 0.2747 \\ \cos \theta =-0.2747 \\ \sin \theta =-3.5\times -0.2747 \\ =0.96145\approx 0.96 \end{gathered}$$