المُدرَّجاتُ التكراريةُ

المُدرَّجاتُ التكراريةُ

Histograms

فكرةُ الدرسِ : تمثيلُ البياناتِ المتصلةِ المُنظَّمةِ في جداولَ تكراريةٍ بمُدرَّجاتٍ تكراريةٍ.

المُخطَّطاتُ التكراريةُ

تعلَّمْتُ سابقًا أنَّ المُخطَّطاتِ التكراريةَ هيَ أكثرُ الطرائقِ شيوعًا لتمثيلِ البياناتِ المتصلةِ والمُمثَّلةِ في جداولَ تكراريةٍ.

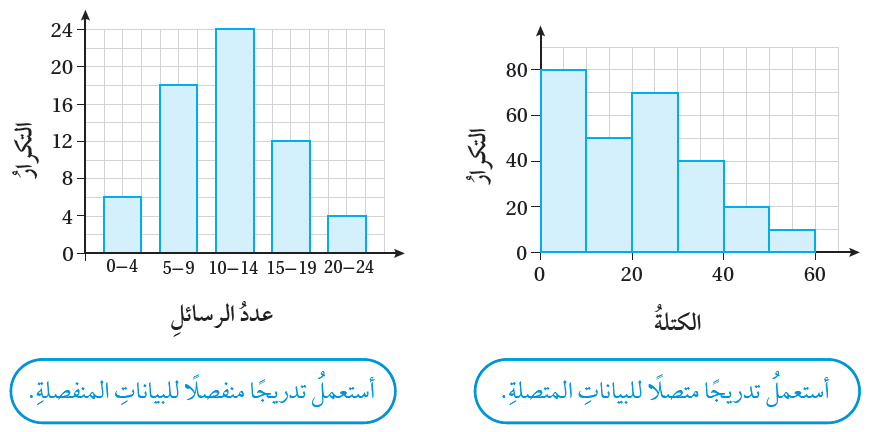
يُطلَقُ على المُخطَّطاتِ التكراريةِ المُستعمَلةِ لعرضِ البياناتِ العدديةِ المتصلةِ والمُمثَّلةِ في جداولَ تكراريةٍ اسمُ المُدرَّجاتِ

التكراريةِ ( histograms ). سأتعلَّمُ في هذا الدرسِ تمثيلَ نوعينِ منْها، هما : المُدرَّجاتُ التكراريةُ ذاتُ الفئاتِ مُتساويةِ

الطولِ، والمُدرَّجاتُ التكراريةُ ذاتُ الفئاتِ غيرِ مُتساويةِ الطولِ.

 

أولًا :  المُدرَّجاتُ التكراريةُ ذاتُ الفئاتِ مُتساويةِ الطولِ

عندَ تمثيلِ البياناتِ العدديةِ المتصلةِ والمُجمَّعةِ في فئاتِ بمُدرَّجاتٍ تكراريةٍ عنْ طريقِ استعمالِ مُدرَّجٍ تكراريٍّ ذي فئاتٍ

مُتساويةِ الطولِ، يجبُ استعمالُ تدريجٍ متصلٍ بالمحورِ الأفقيِّ، وهذا يعني عدمَ وجودِ فراغاتٍ بينَ أعمدةِ المُدرَّجِ.

مثال 1 :

في ما يأتي الزمنَ (بالدقائقِ) مقربًا لأقرب دقيقة الذي يستغرقه مجموعةٌ منْ الطلاب للوصول إلى المدرسة :  

 $$\begin{gathered} 6 18 22 7 25 18 20 10 \\ 12 16 13 12 14 21 26 29 \\ 18 23 17 15 11 14 24 12 18 \end{gathered}$$

a) أُمثِّلُ البياناتِ باستعمالِ مُدرَّجٍ تكراريٍّ ذي فئاتٍ مُتساويةِ الطولِ.

b) أكتبُ وصفًا للبياناتِ.

الحل : 

a) أُمثِّلُ البياناتِ باستعمالِ مُدرَّجٍ تكراريٍّ ذي فئاتٍ مُتساويةِ الطولِ.

الخطوةُ 1 : أُنظِّمُ البياناتِ في جدولٍ تكراريٍّ ذي فئاتٍ متساويةِ الطولِ.

أُحدِّدُ أصغرَ قيمةٍ في البياناتِ، وأكبرَ قيمةٍ فيها. بعدَ ذلكَ أختارُ فئاتٍ مناسبةً تشملُ جميعَ البياناتِ المُستهدَفةِ.

التكرار	الزمن $\left(min\right)$
2	$5 \le t < 10$
8	$10 \le t < 15$
7	$15 \le t < 20$
5	$20 \le t < 25$
3	$25 \le t < 30$

 

الخطوةُ 2 : أرسمُ محورًا أفقيًّا وآخرَ عموديًّا، ثمَّ أكتبُ الفئاتِ أسفلَ المحورِ الأفقيِّ، ثمَّ أضعُ تدريجًا مناسبًا للمحورِ الرأسيِّ. 

الخطوةُ 3 : أُسمّي كُلًّ منَ المحورينِ، ثمَّ أكتبُ عنوانًا مناسبًا للمُدرَّجِ التكراريِّ.

الخطوةُ 4 : أرسمُ عمودًا يُمثِّلُ ارتفاعُهُ تكرارَ كلِّ فئةٍ.

---

 

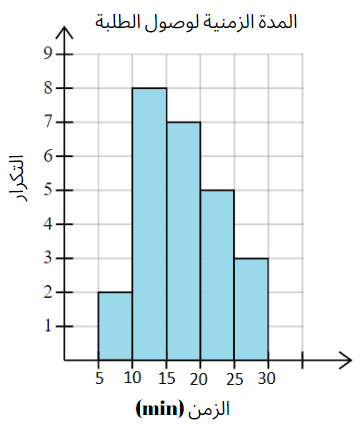
b) أكتبُ وصفًا للبياناتِ.

يستغرق زمن وصول أكثر من نصف الطلبة بين 10 دقائق و 25 دقيقة ، وقليل منهم يصل إلى مدرسته في أقل من 10 دقاثق أو أكثر من 25 دقيقة .

---

ثانيًا : المُدرَّجاتُ التكراريةُ ذاتُ الفئاتِ غيرِ مُتساويةِ الطولِ

في بعضِ الأحيانِ، تُجمَّعُ البياناتُ المتصلةُ في جداولَ تكراريةٍ ذاتِ فئاتٍ غيرِ متساويةٍ في الطولِ. وفي هذهِ الحالةِ، يتعيَّنُ

تمثيلُ هذهِ البياناتِ بمُدرَّجٍ تكراريٍّ ذي فئاتٍ غيرِ مُتساويةِ الطولِ. ولكنْ، إذا مُثِّلَتِ البياناتُ باستعمالِ تكراراتِها، فإنَّ التمثيلَ

الناتجَ يكونُ مُضلِّلًا ؛ لأنَّ النسبةَ بينَ مساحاتِ الأعمدةِ لا تكونُ متناسبةً معَ النسبةِ بينَ التكراراتِ. وهنا تظهرُ الحاجةُ إلى

إيجادِ الكثافةِ التكراريةِ ( frequency density ) لكلِّ فئةٍ، وذلكَ بقسمةِ تكرارِ الفئةِ على طولِها كما يأتي : 

$( \mathrm{التكرارية} \mathrm{الكثافة} ) =\frac{( \mathrm{الفئة} \mathrm{تكرار} )}{( \mathrm{الفئة} \mathrm{طول} )}$

عندَ تمثيلِ الجداولِ التكراريةِ ذاتِ الفئاتِ غيرِ المتساويةِ في الطولِ بمُدرَّجاتٍ تكراريةٍ، فإنَّ المحورَ y يُسمّى الكثافةَ التكراريةَ،

وإنَّ ارتفاعَ كلِّ عمودٍ يُمثِّلُ الكثافةَ التكراريةَ لفئتِهِ.

مثال 2 :

يُبيِّنُ الجدولُ التكراريُّ التالي الزمنَ(بالساعاتِ)الذي يستغرقُهُ 60 شخصٍ يوميًّا في استخدام الانترنت . أُمثِّلُ بياناتِ الجدولِ

باستعمالِ المُدرَّجِ التكراريِّ.

التكرار	الزمن $\left(h\right)$
5	$0 \le h < 1$
7	$1 \le h < 2$
10	$2 \le h < 2.5$
18	$2.5 \le h < 3$
20	$3 \le h < 5$

الحل :

الخطوةُ 1: أُنشِئُ جدولًا بإضافةِ عمودينِ إلى الجدولِ المعطى، أُنظِّمُ فيهما أطوالَ الفئاتِ والكثافةَ التكراريةَ على النحوِ الآتي:

طول الفئة  = الحد الأعلى  -  الحد الأدنى 

$( \mathrm{التكرارية} \mathrm{الكثافة} ) =\frac{( \mathrm{الفئة} \mathrm{تكرار} )}{( \mathrm{الفئة} \mathrm{طول} )}$

الكثافة التكرارية	طول الفئة	التكرار	الزمن $\left(h\right)$
5	1	5	$0 \le h < 1$
7	1	7	$1 \le h < 2$
20	0.5	10	$2 \le h < 2.5$
36	0.5	18	$2.5 \le h < 3$
10	2	20	$3 \le h < 5$

 

 

الخطوةُ 2 : أرسمُ محورًا أفقيًّا وآخرَ عموديًّا، ثمَّ أكتبُ الفئاتِ أسفلَ المحورِ الأفقيِّ، ثمَّ أضعُ تدريجًا مناسبًا للمحورِ الرأسيِّ.
 

الخطوةُ 3 : أُسمّي كُلًّ منَ المحورينِ، ثمَّ أكتبُ عنوانًا مناسبًا للمُدرَّجِ التكراريِّ.

الخطوةُ 4 : أرسمُ عمودًا يُمثِّلُ ارتفاعُهُ الكثافةَ التكراريةَ لكلِّ فئةٍ.

---

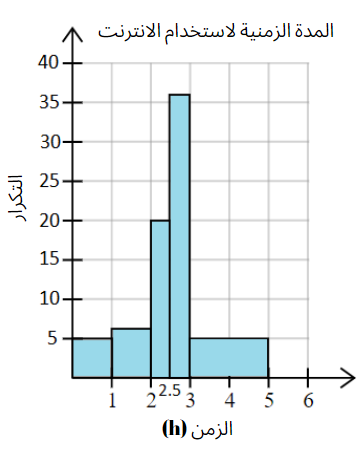
•• يُمكِنُ استعمالُ المُدرَّجاتِ التكراريةِ ذاتِ الفئاتِ غيرِ مُتساويةِ الطولِ لتفسيرِ البياناتِ التي يُمثِّلُها المُدرَّجُ التكراريُّ.

مثال 3 :

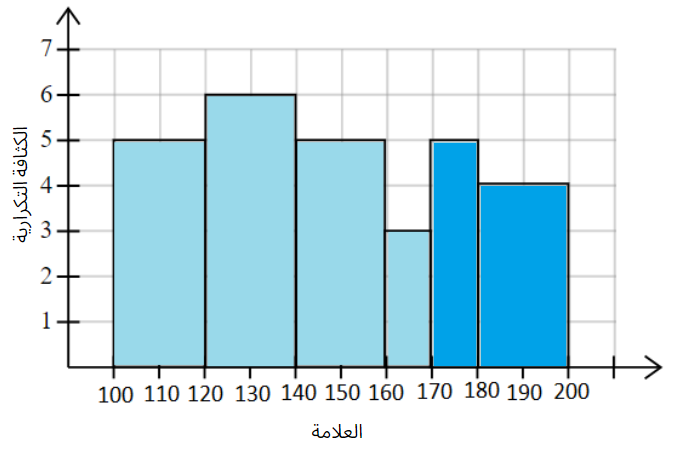
يُبيِّنُ المُدرَّجُ التكراريُّ المجاورُ علاماتِ مجموعةٍ منَ طلبة الثانوية في اختبارٍ نهايتُهُ العظمى هيَ 200 :

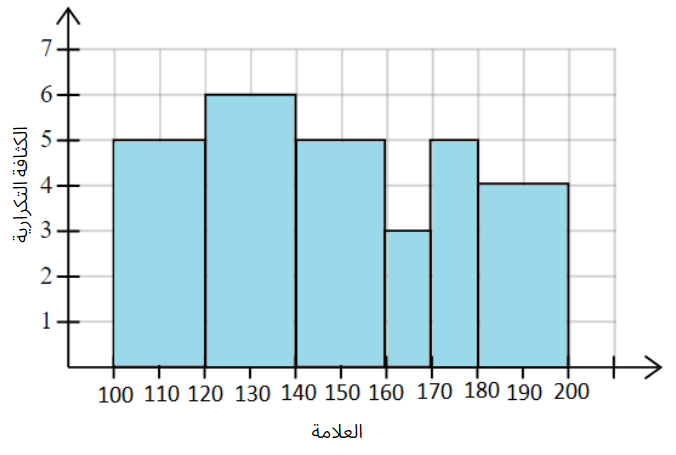a) كمْ طالبًا تقدَّمَ للاختبارِ؟

b) أجدُ عددَ الطلبةِ الذينَ تزيدُ علاماتُهُمْ على 170 .

الحل :

a) كمْ طالبًا تقدَّمَ للاختبارِ؟

بما أنَّ ارتفاعاتِ الأعمدةِ لا تُمثِّلُ التكراراتِ، وإنَّما تُمثِّلُ الكثافةَ التكراريةَ للفئةِ، فإنَّهُ يتعيَّنُ إيجادُ تكرارِ كلِّ فئةٍ، وذلكَ بإيجادِ

مساحةِ كلِّ عمودٍ، علمًا بأنَّ مجموعَ هذهِ المساحاتِ يُمثِّلُ عددَ الطلاب الذينَ تقدموا للاختبار :

مجموعُ مساحاتِ الأعمدةِ	$A = (5\times 20)+(6\times 20)+(5\times 20)+(3\times 10)+(5\times 10)+(4\times 20)$
بالتبسيطِ	$= 480$

 

إذنْ، عدد الطلاب الذين تقدموا  للاختبار هو  480 طالب . 

 

•• أتعلَّمُ ؛  بما أنَّ الكثافةَ التكراريةَ تُمثِّلُ ناتجَ قسمةِ تكرارِ الفئةِ على طولِها، فإنَّهُ يُمكِنُ إيجادُ تكرارِ الفئةِ بضربِ الكثافةِ  التكراريةِ للفئةِ في طولِ الفئةِ، وهذا يُمثِّلُ مساحةَ العمودِ المُمثِّلِ للفئةِ.

 

---

 

b) أجدُ عددَ الطلبةِ الذينَ تزيدُ علاماتُهُمْ على 170 .

لإيجادِ عددِ الطلاب الذينَ تزيدُ علاماتهم على170  أجدُ مساحةَ العمودينِ المُظلَّلينِ باللونِ الأزرقِ الغامقِ في الشكلِ المجاورِ :

 

مجموعُ مساحتيِ العمودينِ	$A = (5\times 10) + (4\times 20)$
بالتبسيطِ	$= 130$

 

إذنْ، عددُ الطلاب الذينَ تزيدُ علاماتهم عن 170 هو 130 طالب.

 

---