المعدلات المرتبطة

         

تعلمت في مرحلة سابقة ان السرعة كمية متجهة تساوي ناتج  قسمة المسافة المقطوعة في وحدة الزمن   ، $v\mathit{=}\frac{s}{t}$  

وأن الاجسام المتحركة والتي تُغيّر موقعها أو أبعادها ، مثل حركة جسيم في خط مستقيم ،

أو تمدُّد أبعاد جسيم ما ستحدث فارقاً بين موقعها الابتدائي (قيمتها الاساسية) ، وقيمتها في لحظة ما .

فإذا تحرك جسيم في خط مستقيم من النقطة  a  إلى النقطة  b .  فإنه يمكن الاصطلاح على تسمية

 هذه المسافة بـ x  ، وأنها احتاجت إلى سرعة ما في وحدة الزمن .وتسمى هذه السرعة معدلاً مرتبطاً بالزمن . كما في الشكل :

                                                                                       

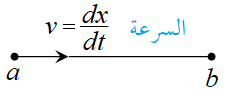
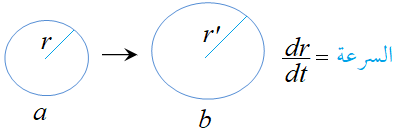
والتمدد في مساحة الدائرة وآنتقالها من الوضع a  إلى الوضع b  . ناتج عن التغيّر في نصف القطر بمرور الزمن كما في الشكل :

                                                                            

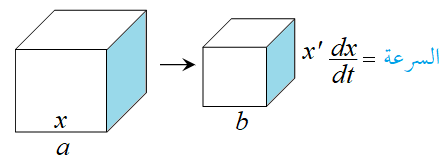
و التقلص في حجم المكعب وآنتقاله من الوضع a  إلى الوضع b  . ناتج عن التغير في طول الضلع بمرور الزمن .كما في الشكل :

                                                                         

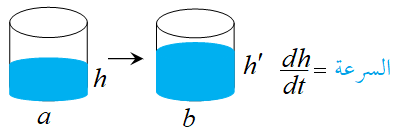
و الزيادة  في حجم السائل وآنتقاله من الوضع a  إلى الوضع b  . ناتج عن التغير في إرتفاع مستوى السائل بمرور الزمن . 

                                                                       

وكذلك نجد أنَّه إذا تحرك الجسم في الاتجاه x  ، فإنَّ   $x\mathit{=}\frac{dx}{dt}t$  .

                                                      وفي الاتجاهy  ، فإنَّ: $y\mathit{=}\frac{dy}{dt}t$ .

ولحل المسائل العملية في هذا التطبيق فيتعيَّن علينا تحديد المعدل المطلوب ولحظة التعويض بعناية فائقة !!

ذلك وأنَّ تحديدهما بدقة سيحدِّد بوضوح مجريات الحل وكيفية إدارة المسألة. فلن يبدأ الاشتقاق ولن يتم التعويض مالم يتم ضبط المطلوب .

فمثلاً :

بفرض أن المطلوب معدل التغيّر في مساحة الدائرة $A$  ، عندما نصف القطر r = a  ،

حيث  a   لحظة التعويض بعد الاشتقاق .    

فيُصاغ المطلوب على النحو التالي :$\frac{dA}{dt}\overline{){}_{when\mathit{ }r\mathit{ }\mathit{=}\mathit{ }a}}\mathit{ }\mathit{ }\mathit{ }$    

لتصبح الحاجة لعلاقة بين A ، r   فقط : وهي $A\mathit{=}\pi \mathit{ }{r}^{\mathit{2}}$  .

فمثلاً :

بفرض أن المطلوب معدل التغيّر في حجم السائل في أسطوانة دائرية قائمة ، ارتفاعها h  .  

عندما يصبح نصف قطرها r = a   حيث a   لحظة التعويض بعد الاشتقاق .    

فيُصاغ المطلوب على النحو التالي : $\frac{dV}{dt}\overline{){}_{when\mathit{ }r\mathit{ }\mathit{=}\mathit{ }a}}\mathit{ }\mathit{ }\mathit{ }$   

لتصبح الحاجة لعلاقة بدلالة  v ، r   : وهي  $v\mathit{=}\pi \mathit{ }{r}^{\mathit{2}}h$  . مما يعني وجوب استبدال المتغير  (   .( h

مثال:                                

أسطوانة دائرية قائمة تتمدَّد بحيث يزداد نصف قطرها بمعدل $\mathit{ }\mathit{2}cm\mathit{/}s$.

فإذا كان أرتفاع الاسطوانة يساوي دائماً مثلي نصف قطرها.

جد معدل التغير في حجم الاسطوانة عندما يصبح نصف قطرها 10 cm .

يصاغ المطلوب على النحو التالي :  $\frac{dV}{dt}\overline{){}_{when\mathit{ }r\mathit{ }\mathit{=}\mathit{10}}}\mathit{ }\mathit{ }\mathit{ }$ 

لتصبح الحاجة لعلاقة بدلالة  r  ، v  فقط : وهي $v\mathit{=}\pi \mathit{ }{r}^{\mathit{2}}h$  .

لاحظ وجود متغير آخر h  يحول دون الاشتقاق والتعويض . فيجب إستبداله بدلالة  r  :

ولكي يتم الاستبدال لا بد من وجود إحدى التالية :

• علاقة مساندة معطاة .

• شكل توضيحي تظهر فيه العلاقة بين المتغيرين (التشابه).

• متطابقة مثلثية في حالة النسب المثلثية .

وفي هذا المثال فالعلاقة المساندة معطاه صراحةً (أرتفاع الاسطوانة يساوي دائماً مثلي نصف قطرها)

       أي أن h = 2r  ، لتصبح علاقة الحجم كالتالي :

                                                                $$\begin{gathered} v\mathit{=}\pi \mathit{ }{r}^{\mathit{2}}h \\ v\mathit{=}\pi \mathit{ }{r}^{\mathit{2}}\mathit{\left(}\mathit{2}r\mathit{\right)} \\ v\mathit{=}\mathit{2}\pi \mathit{ }{r}^{\mathit{3}} \end{gathered}$$          

وأنَّ العلاقة باتت جاهزة للإشتقاق والتعويض كما يلي :

                                                  $$\begin{gathered} v\mathit{=}\mathit{2}\pi \mathit{ }{r}^{\mathit{3}} \\ \frac{dv}{dt}\mathit{=}\mathit{6}\pi \mathit{ }{r}^{\mathit{2}}\frac{dr}{dt} \\ \frac{dv}{dt}\mathit{=}\mathit{6}\pi {\mathit{\left(}\mathit{10}\mathit{\right)}}^{\mathit{2}}\mathit{\left(}\mathit{2}\mathit{\right)} \\ \mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{=}\mathit{1200}\pi \mathit{ }\mathit{ }c{m}^{\mathit{3}}\mathit{/}s \end{gathered}$$          

مثال :

إذا كانت $x^{\mathit{2}}\mathit{+}{y}^{\mathit{2}}\mathit{=}\mathit{100}$  علاقة تربط بين المتغيرين ، وكان المطلوب إيجاد معدل التغير في الاحداثي x  ، عندما x = 6  .

يصاغ المطلوب على النحو التالي :$\frac{dx}{dt}\overline{){}_{x\mathit{ }\mathit{=}\mathit{6}}}\mathit{ }\mathit{ }\mathit{ }$.

لتصبح الحاجة لعلاقة بدلالة  x  : وهي معطاة $x^{\mathit{2}}\mathit{+}{y}^{\mathit{2}}\mathit{=}\mathit{100}$

وستظهر هنا مشكلة في التعويض بقيمة y  بعد الاشتقاق .

والتي ستحل بالعودة إلى العلاقة الأساسية  $x^{\mathit{2}}\mathit{+}{y}^{\mathit{2}}\mathit{=}\mathit{100}$  ، وتعويض قيمة     x = 6لحل قيمة  y  .

ومن الجدير بالذكر أنه يمكننا أن نعبِّر عن كافة المتغيرات بدلالة الزمن في حال اعطيت لحظة التعويض :

عند $t\mathit{=}{t}_{\mathit{1}}$ . وذلك من خلال العلاقات : $x\mathit{=}\frac{dx}{dt}t\mathit{ }\mathit{،}\mathit{ }y\mathit{=}\frac{dy}{dt}t\mathit{ }\mathit{،}\mathit{ }v\mathit{=}\frac{dv}{dt}t\mathit{ }\mathit{.}\mathit{.}\mathit{.}\mathit{.}\mathit{.}$

ومثال ذلك :

 تتحرك نقطة في المستوى الديكارتي حسب العلاقة  $x^{\mathit{2}}\mathit{+}{y}^{\mathit{2}}\mathit{=}\mathit{100}$  ،

فإذا كان معدل التغيّر في الاحداثي x  يساوي $\mathit{3}\mathit{ }cm\mathit{/}s$   ، فما قيمة معدل التغير في الاحداثي y    بعد ثانيتين .

يُصاغ المطلوب على النحو التالي : $\frac{\mathit{d}\mathit{y}}{\mathit{d}\mathit{t}}\overline{)\mathit{t}\mathit{=}\mathit{3}}\mathit{ }\mathit{ }\mathit{ }$

لتصبح الحاجة لعلاقة بدلالة  y  ، t  فقط :

 $x\mathit{=}\frac{dx}{dt}t\mathit{ }\mathit{،}\mathit{ }y\mathit{=}\frac{dy}{dt}t\mathit{ }$   ، فإنَّ :

$$\begin{gathered} x^{\mathit{2}}\mathit{+}{y}^{\mathit{2}}\mathit{=}\mathit{100} \\ y\mathit{=}\sqrt{\mathit{100}\mathit{-}{x}^{\mathit{2}}} \\ \mathit{ }\mathit{ }\mathit{=}\sqrt{\mathit{100}\mathit{-}{\mathit{\left(}\frac{\mathit{d}\mathit{x}}{\mathit{d}\mathit{t}}\mathit{t}\mathit{\right)}}^{\mathit{2}}} \\ \mathit{ }\mathit{ }\mathit{=}\sqrt{\mathit{100}\mathit{-}{\mathit{\left(}\mathit{3}\mathit{t}\mathit{\right)}}^{\mathit{2}}} \\ \mathit{ }\mathit{=}\sqrt{\mathit{100}\mathit{-}\mathit{9}{t}^{\mathit{2}}} \\ \frac{dy}{dt}\mathit{=}\frac{\mathit{-}\mathit{18}t}{\mathit{2}\sqrt{\mathit{100}\mathit{-}\mathit{9}{t}^{\mathit{2}}}} \\ \frac{dy}{dt}\mathit{=}\frac{\mathit{-}\mathit{18}\mathit{\left(}\mathit{2}\mathit{\right)}}{\mathit{2}\sqrt{\mathit{100}\mathit{-}\mathit{9}{\mathit{\left(}\mathit{2}\mathit{\right)}}^{\mathit{2}}}}\mathit{=}\mathit{-}\frac{\mathit{18}}{\mathit{8}}\mathit{=}\mathit{-}\frac{\mathit{9}}{\mathit{4}}cm\mathit{/}s \end{gathered}$$           

ومثال ذلك :

ينزلق سلم طوله $\mathit{10}\mathit{ }m$  ، متكئً على جدار عامودي على سطح الارض بمعدل  $\mathit{3}\mathit{ }cm\mathit{/}s$  ،

جد معدل التغير في الزاوية بين السلم والارض بعد ثانيتن .

يصاغ المطلوب على النحو التالي : $\frac{\mathit{d}\mathit{\theta }}{\mathit{d}\mathit{t}}\overline{){}_{\mathit{w}\mathit{h}\mathit{e}\mathit{n}\mathit{ }\mathit{t}\mathit{=}\mathit{2}}}\mathit{ }\mathit{ }\mathit{ }$

لتصبح الحاجة لعلاقة بدلالة  $\theta$ ، t  فقط : 

وتظهر الحاجة إلى تمثيل العلاقة بين المتغيرات برسم توضيحي كما في الشكل :

      $$\begin{gathered} cos\theta \mathit{=}\frac{x}{\mathit{10}} \\ \mathit{ }x\mathit{=}\frac{dx}{dt}t\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{لكن} \\ x\mathit{=}\mathit{3}t\mathit{ } \\ cos\theta \mathit{=}\frac{x}{\mathit{10}}\mathit{=}\frac{\mathit{3}t}{\mathit{10}}\mathit{=}\frac{\mathit{3}}{\mathit{10}}t\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{العلاقة}\mathit{ }\mathit{لتصبح}\mathit{ }\mathit{ } \\ \mathit{-}sin\theta \frac{d\theta }{dt}\mathit{=}\frac{\mathit{3}}{\mathit{10}} \\ \mathit{\Rightarrow }\frac{d\theta }{dt}\mathit{=}\mathit{-}\frac{\mathit{3}}{\mathit{10}\mathit{ }sin\theta } \end{gathered}$$

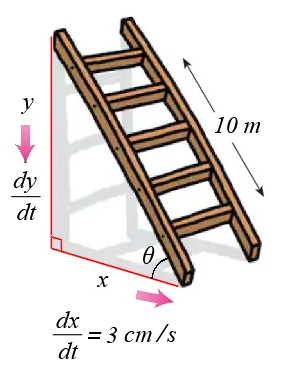
لتصبح الحاجة الآن حل قيمة $\mathit{ }sin\theta$ من متطابقة مثلثية :

$$\begin{gathered} cos\theta \mathit{=}\frac{\mathit{3}}{\mathit{10}}t\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ } \\ \mathit{ }cos\theta \mathit{=}\frac{\mathit{6}}{\mathit{10}}\mathit{=}\frac{\mathit{3}}{\mathit{5}}\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }when\mathit{ }t\mathit{=}\mathit{2}\mathit{ }\mathit{ } \\ \mathit{ }{\mathit{sin}}^{\mathit{2}}\theta \mathit{+}\mathit{ }co{s}^{\mathit{2}}\theta \mathit{=}\mathit{1} \\ si{n}^{\mathit{2}}\theta \mathit{=}\mathit{1}\mathit{-}{\mathit{\left(}\frac{\mathit{3}}{\mathit{5}}\mathit{\right)}}^{\mathit{2}} \\ \mathit{\Rightarrow }si{n}^{\mathit{2}}\theta \mathit{=}\frac{\mathit{16}}{25}\mathit{ }\mathit{ }\mathit{ }\mathit{\Rightarrow }\mathit{ }sin\theta \mathit{=}\frac{\mathit{4}}{\mathit{5}}\mathit{ } \end{gathered}$$         

بالعودة والتعويض :                                                                                                                    $\mathit{\Rightarrow }\frac{d\theta }{dt}\mathit{=}\mathit{-}\frac{\mathit{3}}{\mathit{10}\mathit{ }sin\theta }\mathit{=}\mathit{-}\frac{\mathit{3}}{\mathit{10}\mathit{\times }\mathit{\left(}{\displaystyle \frac{4}{5}}\mathit{\right)}}\mathit{=}\mathit{-}\frac{\mathit{3}}{\mathit{8}}\mathit{ }rad\mathit{/}s$

ومن الامثلة الهامة : حركة جسيم ما على محيط الدائرة أو على جزء منه (الحركة الدائرية):

فالجسم المتحرك على محيط الدائرة نصف قطرها( $\mathit{ }r$ ثابت) سيقطع قوساً طوله $l$ ، والذي يقابل زاوية مركزية قياسها $\theta$ .

حسب العلاقة $\mathit{ }l\mathit{=}r\mathit{ }\theta$ .وباشتقاق العلاقة نجد أنَّ :  $\mathit{ }\frac{dl}{dt}\mathit{=}r\frac{d\theta }{dt}$

                                                                             

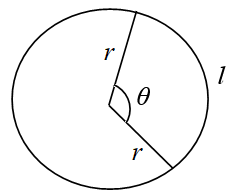
ولإيجاد قيمة $\frac{d\theta }{dt}$ :

$\frac{d\theta }{dt}\mathit{=}\frac{\theta }{t}\mathit{=}\frac{\mathit{2}n\pi }{t}\mathit{ }\mathit{ }$     حيث n عدد الدورات في الدقيقة

مثال:

إذا كانت النقطة a تتحرك بمعدل ربع دورة في الدقيقة بإتجاه عكس عقارب الساعة .

في دائرة نصف قطرها $\mathit{8}\mathit{ }cm$ . جد معدل التغير في زاوية القطاع الناتج عن حركة النقطة .

         $\frac{d\theta }{dt}\mathit{=}\frac{\theta }{t}\mathit{=}\frac{\mathit{2}\pi \mathit{\left(}{\displaystyle \frac{1}{4}}\mathit{\right)}\mathit{\left(}\mathit{8}\mathit{\right)}}{\mathit{1}}\mathit{=}\mathit{4}\pi \mathit{ }rad\mathit{/}min$ 

 

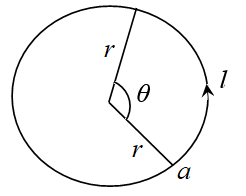
مما سبق يمكن أن نخلص إلى ما يلي :

يستخدم الاشتقاق بقواعده المختلفة والاشتقاق الضمني في حل المسائل العملية والتي تحتوي على كميات تتغير مع الزمن. 

ومن الأمثلة على هذه المسائل، مواقف حياتية تتضمن معدّلات تغيّر كميات النسبة إلى الزمن، مثل:

1. معدّل تغيّر المحيط والمساحة والحجم بالنسبة إلى الزمن.

2. معدّل تغيّر المسافة بالنسبة إلى الزمن.

3. معدّل تغيّر قياس الزاوية بالنسبة إلى الزمن.

4. الحركة الدائرية ومعدّل تغيّر الموقع بالنسبة إلى الزمن.

5. ميكانيكا الحركة وسرعة أجزاء متحركة في الآلات الميكانيكية.

6. معدّل تغيّر حجم الموائع في الوعاء بالنسبة إلى الزمن.

7. معدّل تغيّر درجة الحرارة بالنسبة إلى الزمن.

8. معدّل تغير المقاومة الكهربائية وجهد الدائرة الكهربائية بالنسبة إلى الزمن.

أما استراتيجية حل المسائل المرتبطة، فيمكن تلخيصها بالخطوات التالية:

1. فهم المسألة:

    بتحديد المعطيات.والمطلوب ، والمعدّلات المرتبطة والمُتضمنة في المسألة.

2. تمثيل المسألة: يرسم مخطط توضيحي للمسألة يتضمن معطيات المسألة مع تحديد القيم الثابتة ( بقيمها) والمتغيرة (برموز مناسبة).

3. تحديد العلاقة المناسبة: بناءً على الكمية المطلوبة إيجاد معدّلها بالنسبة إلى الزمن، والمعدلات المعطاة.

4. الاشتقاق بالنسبة إلى الزمن: باستخدام قاعدة السلسلة والاشتقاق الضمني وقواعد الاشتقاق.

5. التعويض في المعادلة الناتجة بالقيم المعطاة لإيجاد المطلوب من المسألة.