نتاجات الدرس:
إيجاد المشتقة الثانية للاقتران.
تصنيف النقاط الحرجة باستعمال اختبار المشتقة الثانية.
إيجاد السرعة المتجهة والتسارع لجسم يتحرك في مسار مستقيم.
المشتقة الثانية:
يُطلق على الاقتران الناتج من اشتقاق الاقتران مرتين اسم المشتقة الثانية، أو اقتران المشتقة الثانية ، ويرمز إليه بالرمز أو .
مثال (1) : جد المشتقة الثانية لكل اقتران مما يأتي:
| b) | a) |
الحل:
a)
b)
- تدريب: جد المشتقة الثانية لكل اقتران مما يأتي :
| b) | a) |
• تصنيف القيم الحرجة باستعمال اختبار المشتقة الثانية :

مثال (2) : إذا كان: ، فأستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران f .
الحل:
نلاحظ ان أذن توجد قيمة عظمى محلية عندما وهي:
نلاحظ ان أذن توجد قيمة صغرى محلية عندما وهي:
- تدريب: إذا كان : f(x)=x^5-5x^3 ، فأستعمل اختبار المشتقة الثانية لإيجاد القيم القصوى المحلية للاقتران f .
- تمثيل اقترانات كثيرات الحدود بيانياً :
يساعد إيجاد النقاط الحرجة للاقتران وتحديد نوعها باستعمال اختبار المشتقة الثانية ، عند تمثيل اقترانات كثيرات الحدود بيانياً ، فهو يعطي تصوراً لشكل منحنى الاقتران .
مثال (3): مثل الاقتران بيانيا
الحل:
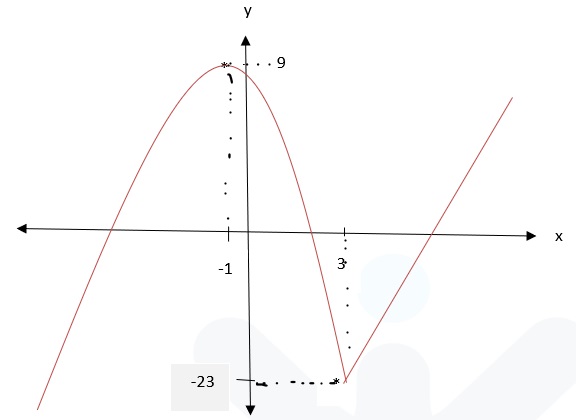 |
|
تدريب: مثل الاقتران بيانيا:
السرعة والتسارع عند الحركة في مسار مستقيم:
|
عند دراسة جسم يتحرك في مسار مستقيم، أفترض أنَّ الجسم يتحرك على خط أعداد انطلاقا من موقع ابتدائي، وأن اتجاه حركته يكون موجباً أو سالباً ، وأن موقع الجسم بالنسبة إلى نقطة الأصل يُمثل اقترانا بالنسبة إلى الزمن t، ويُرمز إليه بالرمز s(t). يُطلق على المشتقة الأولى لاقتران الموقع s(t) اسم السرعة المتجهة للجسم، ويُرمز إليها بالرمز v(t) وقد سميت بهذا الاسم لأنها تُستعمل لتحديد سرعة الجسم واتجاه حركته، فإذا كانت قيمة فإنَّ الجسم يتحرك في الاتجاه الموجب، وإذا كانت قيمة فإنَّ الجسم يتحرك في الاتجاه السالب، وإذا كانت فإنَّ الجسم يكون في حالة سكون. يُطلق على المشتقة الثانية لاقتران الموقع s(t) اسم التسارع ، ويُرمز إليها بالرمز a(t) |
مثال (4): يمثل الاقتران: موقع جسم يتحرك في مسار مستقيم ، حيث s الموقع بالأمتار ، و t الزمن بالثواني :
1) ما سرعة الجسم عندما t=3 ؟
2) في أي اتجاه يتحرك الجسم عندما t=3 ؟
3) ما تسارع الجسم عندما t=3 ؟
4) جد قيم t التي يكون عندها الجسم في حالة سكون لحظي .
الحل:
1)
اذن ، سرعة الجسم عندما t=3 هي:
2) بما أن اشارة السرعة سالبة عندما t=3 فإنّ الجسم يتحرك في الاتجاه السالب عند تلك اللحظة.
3)
اذن ، تسارع الجسم عندما t=3 هو:
4)
يكون الجسم في حالة سكون لحظي عندما
• توجد تطبيقات حياتية عديدة للسرعة والتسارع ، ويمكن استعمال هذه التطبيقات لتحليل حركة الأجسام .
مثال (5): يمكن نمذجة موقع فهد يطارد فريسته على أرض مستوية متحركاً في خط مستقيم باستعمال الاقتران: ، حيث t الزمن بالثواني ، و s الموقع بالأمتار :
1) ما سرعة الفهد بعد 3 ثوان من بدء حركته؟
2) ما تسارع الفهد بعد 3 ثوان من بدء حركته؟
3) جد قيم t التي يكون عندها الفهد في حالة سكون لحظي؟
الحل:
1)
إذن، سرعة الفهد بعد 3 ثوان من بدء حركته هي :
2)
إذن، تسارع الفهد بعد 3 ثوان هو :
3)
يكون الفهد في حالة سكون لحظي عندما
- تدريب: يتحرك سليم في مسار مستقيم على لوح تزلج ، بحيث يمكن نمذجة موقعه باستعمال الاقتران: ، حيث t الزمن بالثواني ، و s الموقع بالأمتار:
1) ما سرعة سليم بعد 6 ثوان من بدء حركته؟
2) ما تسارع سليم بعد 6 ثوان من بدء حركته؟
3) جد قيم t التي يكون عندها سليم في حالة سكون لحظي؟