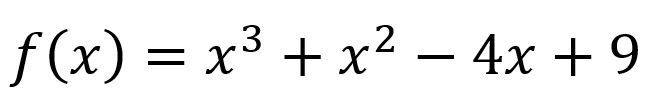المساحة

الدرس الرابع: المساحة

 

سنتعرف في درس المساحة إلى:

طريقة استخدام التكامل في إيجاد مساحة المنطقة المحصورة بين منحنى اقتران والمحور $x$ ؛ حيث يوجد ثلاث حالات للمنطقة المحصورة وهي:

1) تقع فوق المحور $x$ .

2) تقع أسفل المحور  $x$.

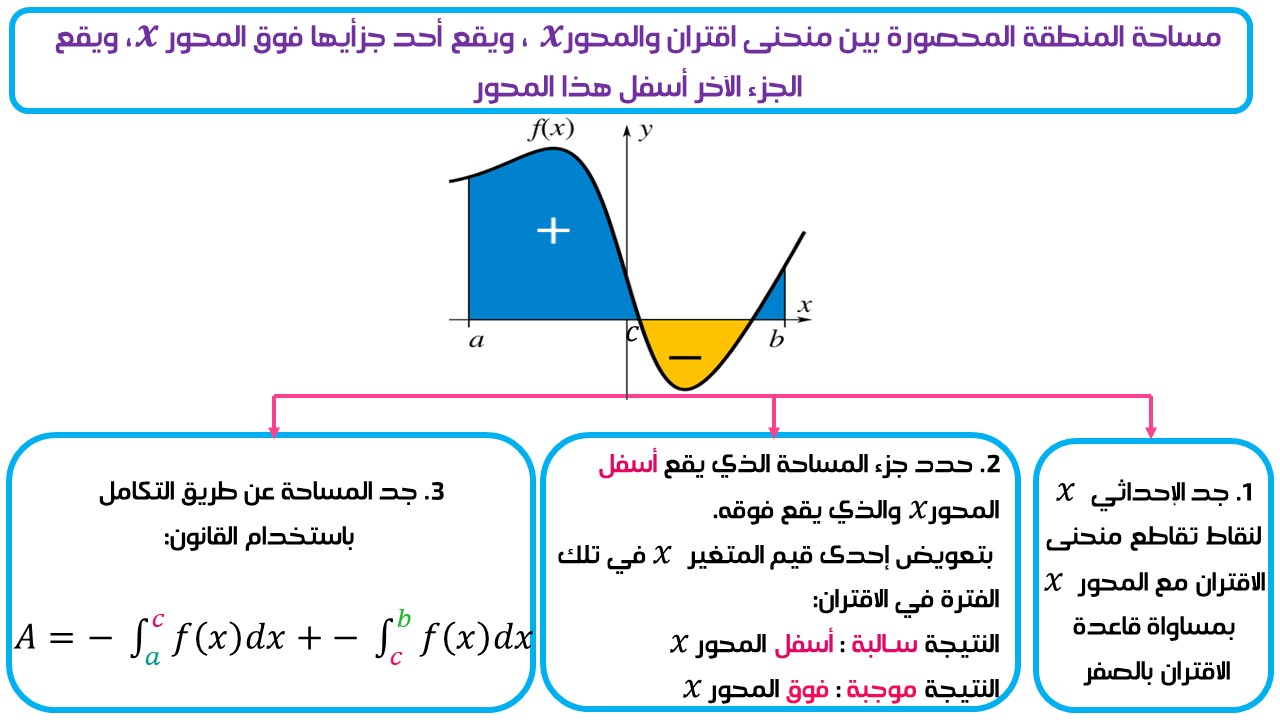
3) يقع أحد جزئيها فوق المحور $x$ ، ويقع الجزء الآخر أسفل هذا المحور.

 

ويمكن تلخيصها بالمخطط الآتي، قبل البدء بالشرح المفصل:

 

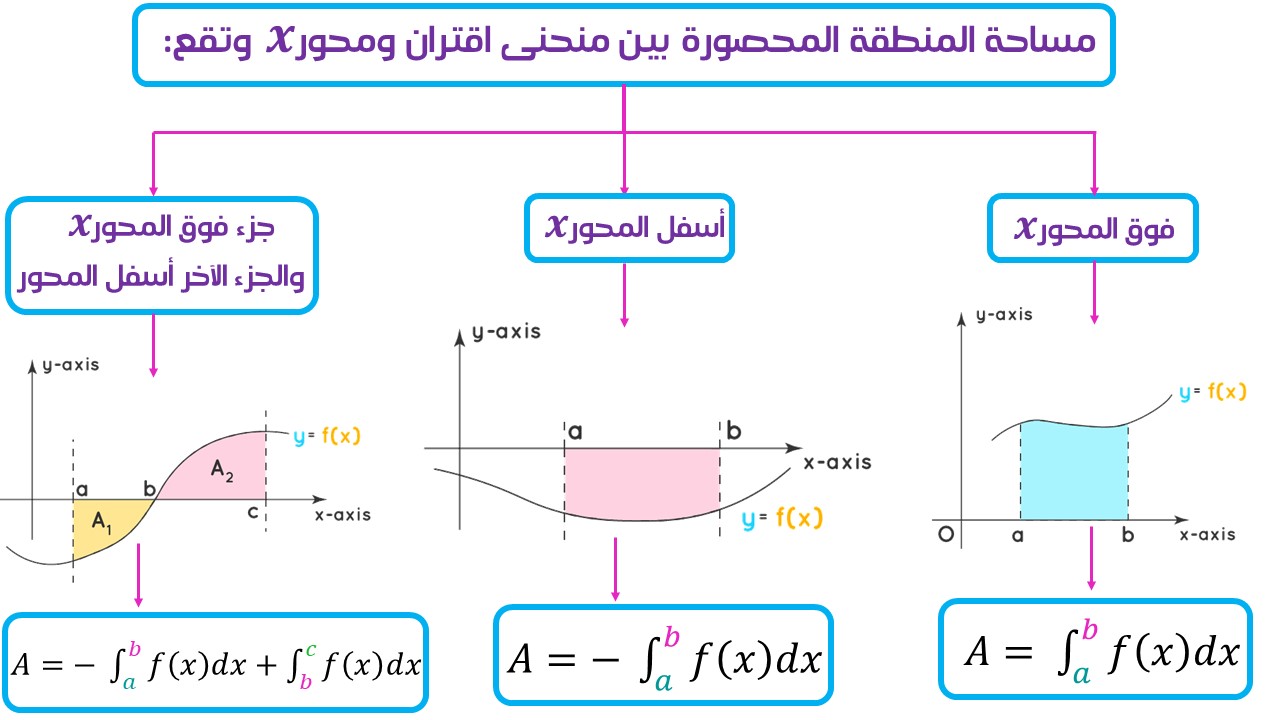
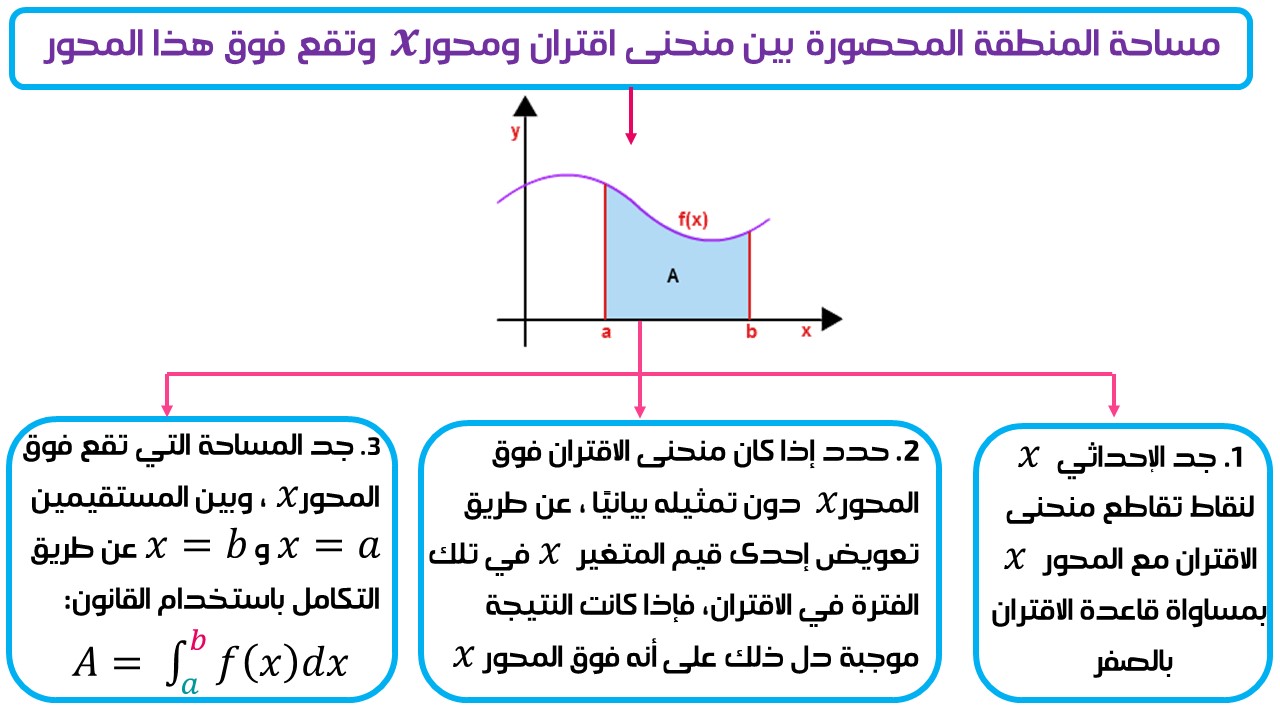
أولًا: مساحة المنطقة المحصورة بين منحنى اقتران والمحور $x$ ، وتقع فوق هذا المحور:

 

يمكن إيجاد المساحة المحصورة بين منحنى الاقتران $f\left(x\right)$ ، و المحور $x$ ، والمستقيمين $x=a$ و $x=b$

وتقع فوق المحور $x$ ، كما في الشكل الآتي:

 

                                                    

 

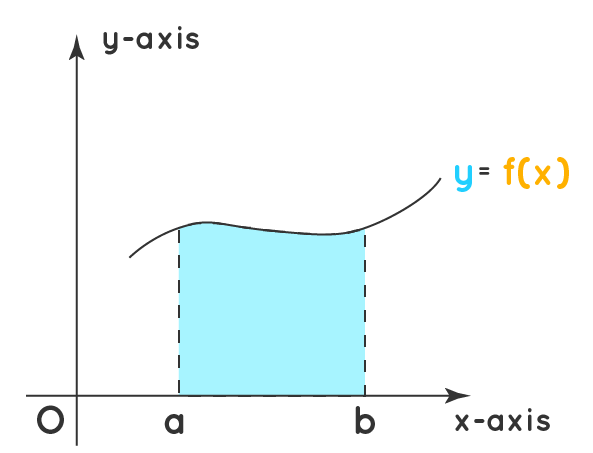
عن طريق التكامل :  $A = {\int }_a^b f\left(x\right) dx ; a< b$

 

وباتباع الخطوات الآتية:

 

 

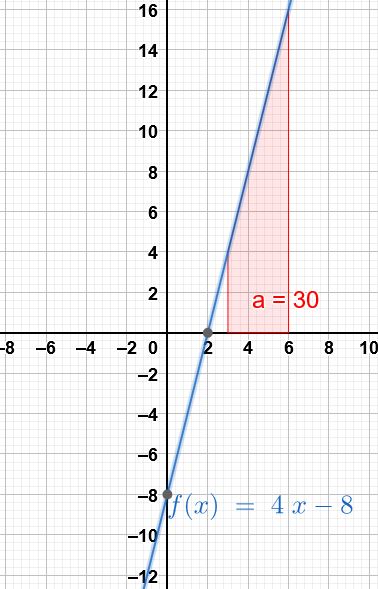
مثال(1): جد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=4x-8$ ، والمحور $x$ ،

              والمستقيمين $x=3$ و $x=6$ .

 

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$ - إن وجدت -
$f\left(x\right) = 0$	بمساواة قاعدة الاقتران بالصفر
$4x-8 = 0$	بتعويض $f\left(x\right)=4x-8$
$\to x = 2$	بحل المعادلة
إذن الإحداثي $x$ لنقطة تقاطع الاقتران $f\left(x\right)$ مع المحور  $x$  لا يقع ضمن الفترة المعطاة
الخطوة 2: جد المساحة عن طريق التكامل المساحة تقع فوق المحور $x$ كما في الشكل السابق.
$A = {\int }_a^b f\left(x\right) dx$	قانون المساحة المحصورة بين منحنى الاقتران والمحور x وتقع فوق هذا المحور
$={\int }_3^6 (4x-8) dx$	بالتعويض $f\left(x\right)= 4x-8 , a=3 , b = 6$
$$\begin{gathered} =\left(\frac{4x^2}{2}-8x\right) \overline{)\begin{array}{c}6\\ 3\end{array} } \\ =\left(2x^2 -8x\right) \overline{)\begin{array}{c}6\\ 3\end{array} } \end{gathered}$$	تكامل اقتران القوة وتكامل الثابت
$=\left(2{\left(6\right)}^2 -8\left(6\right)\right)-\left(2{\left(3\right)}^2 -8\left(3\right)\right)$	بالتعويض
$$\begin{gathered} =\left(2\left(36\right) -48\right)-\left(2\left(9\right) -24\right) \\ =\left(72-48\right)-\left(18-24\right) \\ =24 +6 \\ =30 \end{gathered}$$	بالتبسيط
إذن، المساحة هي: 30 وحدة مربعة.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

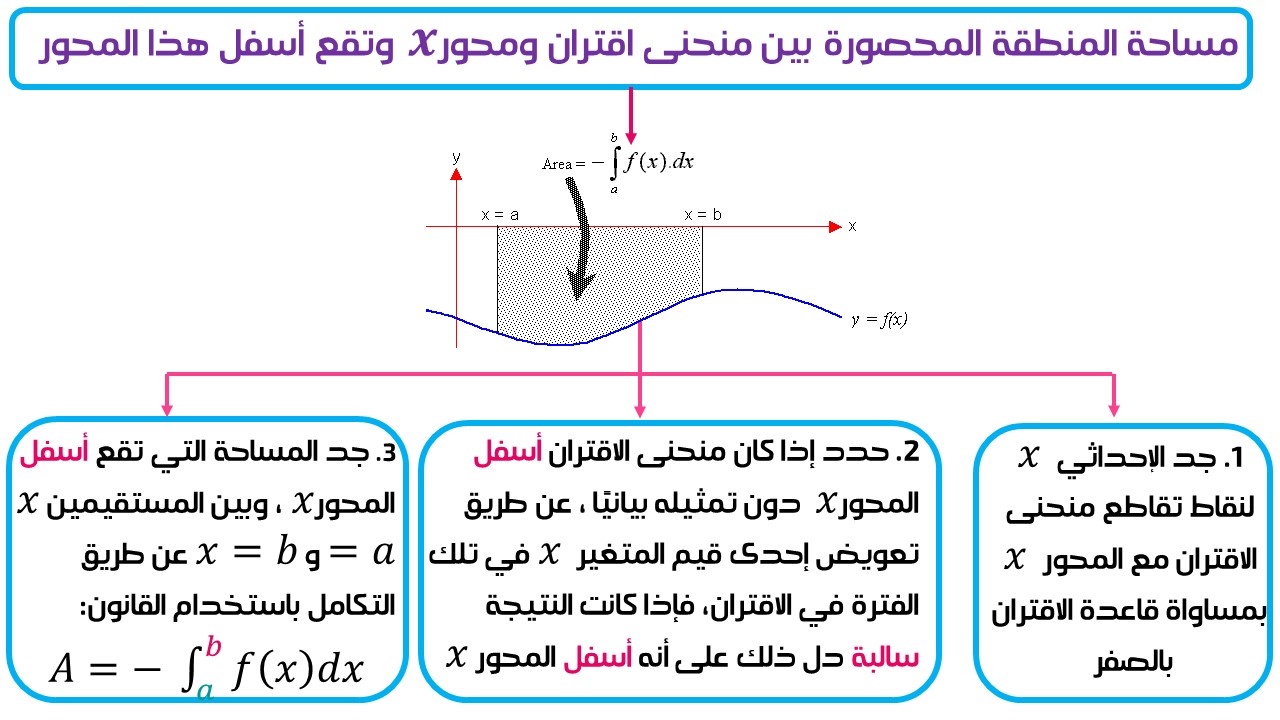
ثانيًا: مساحة المنطقة المحصورة بين منحنى اقتران والمحور $x$ ، وتقع أسفل هذا المحور:

 

يمكن إيجاد المساحة المحصورة بين منحنى الاقتران $f\left(x\right)$ والمحور $x$ ، والمستقيمين: $x=a$،و $x=b$،

وتقع أسفل المحور $x$ كما في الشكل الآتي:

 

 

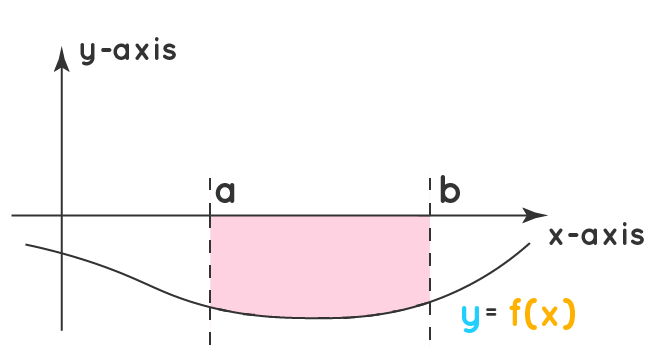
عن طريق التكامل : $A =- {\int }_a^b f\left(x\right) dx ; a< b$

 

ملاحظة: وُضعت الإشارة السالبة قبل التكامل لأن المساحة لا يمكن أن تكون سالبة.

               حيث أن المنطقة التي يراد إيجاد مساحتها تقع أسفل المحور $x$، لذلك فإن قيمة التكامل

              الناتج ستكون عددًا سالبًا؛ لذا يُختار معكوس ناتج التكامل لتكون المساحة موجبة.

 

 

ويمكن إيجاد المساحة باتباع الخطوات الآتية:

 

مثال(2): جد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right) = x^2-9$ والمحور $x$،

              والمستقيمين:$x=1$ , $x=-1$.

 

الحل:

الخطوة 1: جد الإحداثي $x$  لنقاط تقاطع منحنى الاقتران مع المحور $x$ - إن وجدت -
$f\left(x\right) = 0$	بمساواة قاعدة الاقتران بالصفر
$x^2 - 9 = 0$	بتعويض $f\left(x\right) = x^2-9$
$x= 3 or x= -3$	بحل المعادلة التربيعية
إذن الإحداثي $x$ لنقطة تقاطع الاقتران $f\left(x\right)$ مع المحور $x$ لا يقع ضمن الفترة المعطاة.
الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$
$$\begin{gathered} f\left(0\right) = {\left(0\right)}^2-9 \\ = -9 \end{gathered}$$	بتعويض إحدى قيم المتغير x في في الفترة $\left[-1, 1\right]$ في الاقتران
إذن منحنى الاقتران أسفل المحور x لأن نتيجة التعويض سالبة.
الخطوة 3: جد المساحة عن طريق التكامل
$A =- {\int }_a^b f\left(x\right) dx$	قانون المساحة المحصورة بين منحنى الاقتران والمحور x وتقع أسفل هذا المحور
$A =- {\int }_{-1}^{ 1} \left(x^2-9\right) dx$	بالتعويض $f\left(x\right)= x^2-9 , a=-1 , b =1$
$=-\left(\frac{x^3}{3}-9x\right) \overline{)\begin{array}{c} 1\\ -1\end{array}}$	تكامل اقتران القوة وتكامل الثابت
$=- \left(\left(\frac{{\left(1\right)}^3}{3}-9\left(1\right)\right)-\left(\frac{{\left(-1\right)}^3}{3}-9\left(-1\right)\right)\right)$	بالتعويض
$$\begin{gathered} =- \left(\left(\frac{1}{3}-9\right)-\left(\frac{-1}{3}+9\right)\right) \\ =-\left(\frac{1}{3}-9+\frac{1}{3}-9\right) \\ =-\left(\frac{2}{3}-18\right) \\ =-\frac{2}{3}+\frac{54}{3} \\ =\frac{52}{3}\approx 17.3 \end{gathered}$$	بالتبسيط
إذن، المساحة هي تقريبًا: 17 وحدة مربعة.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

ثالثًا: مساحة المنطقة المحصورة بين منحنى اقتران والمحور $x$،

        ويقع أحد جزأيها فوق المحور $x$ ، ويقع الجزء الآخر أسفل هذا المحور :

 

يمكن إيجاد المساحة المحصورة بين:

  منحنى اقتران يقع أحد جزأيه أسفل المحور $x$ والآخر فوق المحور ، والمحور $x$ كما في الشكل الآتي: 

 

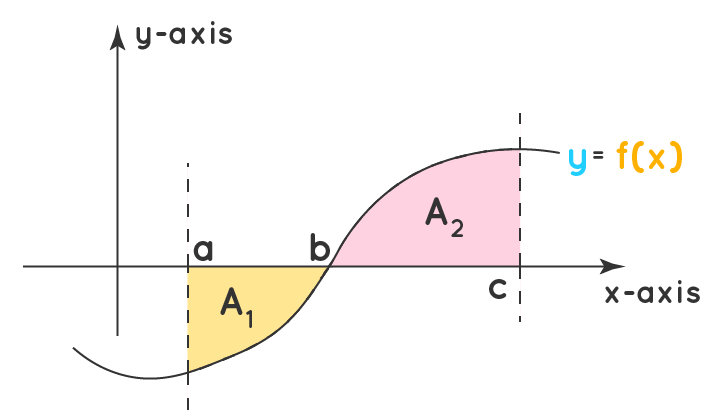
عن طريق التكامل : $A = - {\int }_a^b f\left(x\right) dx + {\int }_b^c f\left(x\right) dx$

 

ويمكن إيجاد المساحة باتباع الخطوات الآتية:

 

 

 

 

 

 

 

 

 

 

 

 

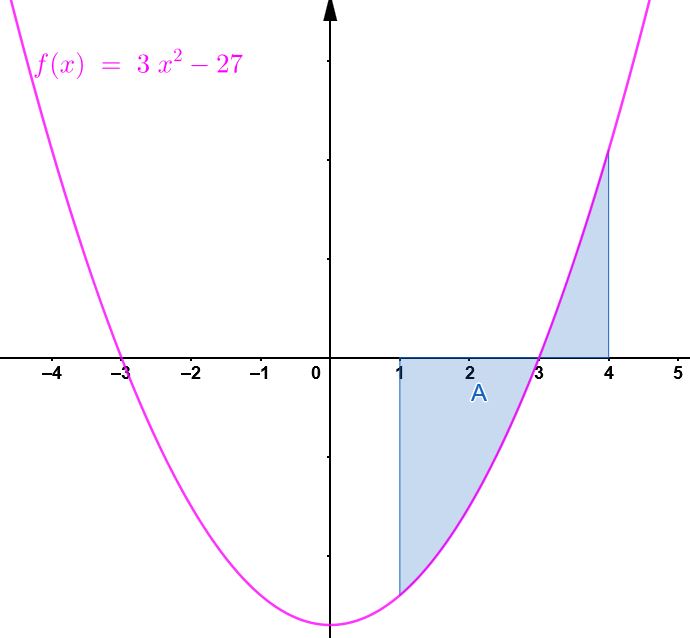
مثال(3): جد مساحة المنطقة المحصورة بين منحنى الاقتران:$f\left(x\right)=3x^2-27$ ،

               والمحور $x$، والمستقيمين:$x=4$، و$x=1$

 

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$                   - إن وجدت -

بمساواة قاعدة الاقتران بالصفر                      $f\left(x\right) = 0$

بتعويض  $f\left(x\right)=3x^2-27$                                $3x^2-27 = 0$

بقسمة طرفي المعادلة على 3                          $x^2-9 = 0$

بتحليل الفرق بين مربعين                                 $(x+3)(x-3)=0$

خاصية الضرب الصفري                                   $x+3=0 or x-3 = 0$

بحل كل معادلة لـــ x                                          $\to x= -3 , x=3$

إذن، $x=3$ يقع ضمن الفترة $\left[1, 4\right]$ كما في الشكل الآتي:

الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$                             (يمكن الاعتماد على الرسم السابق)

بتعويض إحدى قيم المتغير x في في الفترة $[1, 3)$ في الاقتران ولتكن (2) $$\begin{gathered} f\left(2\right)=3{\left(2\right)}^2-27 \\ = 3\left(4\right)-27 \\ =12-27 \\ = -15 <0 \end{gathered}$$ بما أن الناتج سالب فإن الاقتران بالفترة $[1, 3)$ يقع أسفل المحور x ملاحظة: لا يتم تعويض (3) لأنها صفر للاقتران وتقع على محور x

بتعويض إحدى قيم المتغير x في في الفترة $(3, 4]$ في الاقتران ولتكن (4) $$\begin{gathered} f\left(4\right)=3{\left(4\right)}^2-27 \\ = 3\left(16\right)-27 \\ =48-27 \\ = 21 >0 \end{gathered}$$ بما أن الناتج موجب فإن الاقتران بالفترة $(3, 4]$ يقع فوق المحور $x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

الخطوة 3: جد المساحة عن طريق التكامل:

بتجزئة المساحة إلى مجموع مساحتين فوق المحور x وأسفله:

                                                          $A = -{\int }_1^3 (3x^2-27) dx + {\int }_3^4 (3x^2-27) dx$

باستخدام تكامل اقتران القوة المضروب في ثابت، وتكامل الثابت:

                         $=-(\frac{3x^3}{3}-27x) \overline{)\begin{array}{c}3\\ 1\end{array}} + (\frac{3x^3}{3}-27x) \overline{)\begin{array}{c}4\\ 3\end{array}}$

 

بالتبسيط       $=(27x-x^3) \overline{)\begin{array}{c}3\\ 1\end{array}} + (x^3-27x) \overline{)\begin{array}{c}4\\ 3\end{array}}$

بالتعويض     $=\left(\right(27\left(3\right)-{\left(3\right)}^3)-(\left(27\right(1)-{\left(1\right)}^3\left)\right) + \left(({\left(4\right)}^3-27\left(4\right)) -({\left(3\right)}^3-27\left(3\right))\right)$

 

بالتبسيط       $$\begin{gathered} =\left((81-27)-(27-1)\right) + \left((64-108) -(27-81)\right) \\ =(54-26) + (-44 +54) \\ =28+10 \\ =38 \end{gathered}$$ 

 

إذن، المساحة هي 38 وحدة مربعة.

---

 

رابعًا: مساحة المنطقة المحصورة بين منحنى اقتران والمحور $x$، ولا تكون محدودة بمستقيمين:

 

عند إيجاد مساحة المنطقة المحصورة بين منحنى الاقتران والمحور $x$ فقط،

وليست محدودة بمستقيمين - كما في الحالات السابقة - :

1. جد الإحداثي $x$ لنقاط تقاطع الاقتران مع المحور $x$؛ lمن خلال مساواة الاقتران بالصفر وحل المعادلة.

2. حل المعادلة تمثل حدود التكامل.

3. حدد إذا كانت المساحة المطلوبة أسفل أو فوق المحور $x$.

4. استخدم قانون التكامل لإيجاد المساحة.

 

 

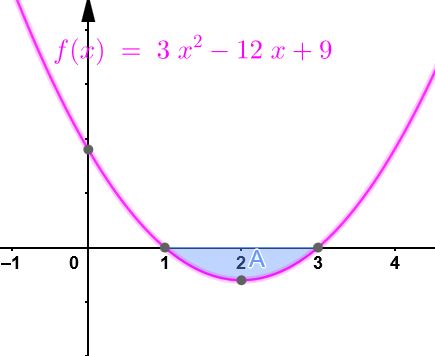
مثال(4): جد مساحة المنطقة المحصورة بين منحنى الاقتران:

                $f\left(x\right)=3x^2 -12x +9$ ،والمحور $x$.

 

الحل:

الخطوة 1: جد الإحداثي $x$ لنقاط تقاطع منحنى الاقتران مع المحور $x$
$f\left(x\right)=0$	بمساواة قاعدة الاقتران بالصفر
$3x^2 -12x +9=0$	بتعويض$f\left(x\right)=3x^2 -12x +9$
$x^2 -4x +3=0$	بقسمة طرفي المعادلة على 3
$\left(x-3\right)\left(x-1\right)=0$	بتحليل الفرق بين مربعين
$x-3=0 or x-1=0$	خاصية الضرب الصفري
$x=3 x=1$	بحل كل معادلة لـــ x
إذن، الإحداثي $x$ لنقاط التقاطع منحنى الاقتران $f\left(x\right)$ مع المحور $x$ هو: $x=3, x=1$ ، كما في الشكل الآتي، وهذان الإحداثيان يمثلان حدي التكامل.
الخطوة 2: حدد إذا كان منحنى الاقتران أسفل أو أعلى المحور $x$                             (يمكن الاعتماد على الرسم السابق)
$$\begin{gathered} f\left(2\right)=3{\left(2\right)}^2-12\left(2\right)+9 \\ = 3\left(4\right)-24 +9 \\ =12-24+9 \\ = -3 \end{gathered}$$	بتعويض إحدى قيم المتغير x في في الفترة $\left(1, 3\right)$ في الاقتران ولتكن (2)
بما أن ناتج التعويض سالب فإن الاقتران بالفترة $(1, 3)$ يقع أسفل المحور x
الخطوة 3: جد المساحة عن طريق التكامل
$A =- {\int }_a^b f\left(x\right) dx$	قانون المساحة المحصورة بين منحنى الاقتران والمحور x وتقع أسفل هذا المحور
$A =- {\int }_1^3 \left(3x^2-12x +9\right) dx$	بالتعويض $$\begin{gathered} f\left(x\right)= 3x^2-12x +9 , \\ a=1 , b =3 \end{gathered}$$
$= - \left(\frac{3x^3}{3}-\frac{12x^2}{2}+9x\right) \overline{)\begin{array}{c}3\\ 1\end{array}}$	تكامل اقتران القوة المضروب في ثابت، وتكامل الثابت
$=(-x^3+6x^2-9x) \overline{)\begin{array}{c}3\\ 1\end{array}}$	بالتبسيط
$=(-{\left(3\right)}^3+6{\left(3\right)}^2-9\left(3\right))-(-{\left(1\right)}^3+6{\left(1\right)}^2-9(1\left)\right)$	بالتعويض
$$\begin{gathered} =(-\left(27\right)+6\left(9\right)-27)-(-1+6-9) \\ =\left(-54+54\right)-\left(-4\right) \\ =4 \end{gathered}$$	بالتبسيط
إذن، المساحة هي 4 وحدة مربعة.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

خامسًا: معمل برمجية جيوجبرا: تطبيقات التكامل : المساحة:

 

يمكن استعمال برمجية جيوجبرا لإيجاد المساحة بين منحنى الاقتران والمحور x 

بوصفها تكاملًا محدودًا، مراعيًاما يأتي:

 

1. إذا وقعت المنطقة أسفل المحور x : حول إشارة الناتج السالبة إلى موجبة.

 

2. إذا كان هنالك منطقتين إحداهما فوق المحور x ، والأخرى تحته:

أ. قسم هذه المنطقة إلى جزأين.

ب. احسب مساحة كل جزء على حدة.

ج. اجمع المساحتين معًا.

 

مثال(5):جد مساحة المنطقة المحصورة بين منحنى الاقتران:

                                             

             ، والمحور x ، والمستقيمين:$x=-3$  و $x=1$

 

الحل:

1. اكتب الاقتران في شريط الإدخال، ثم اضغط (Enter)

 

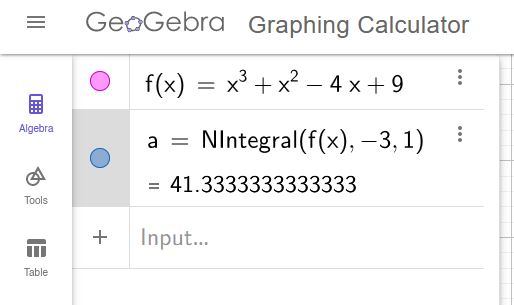
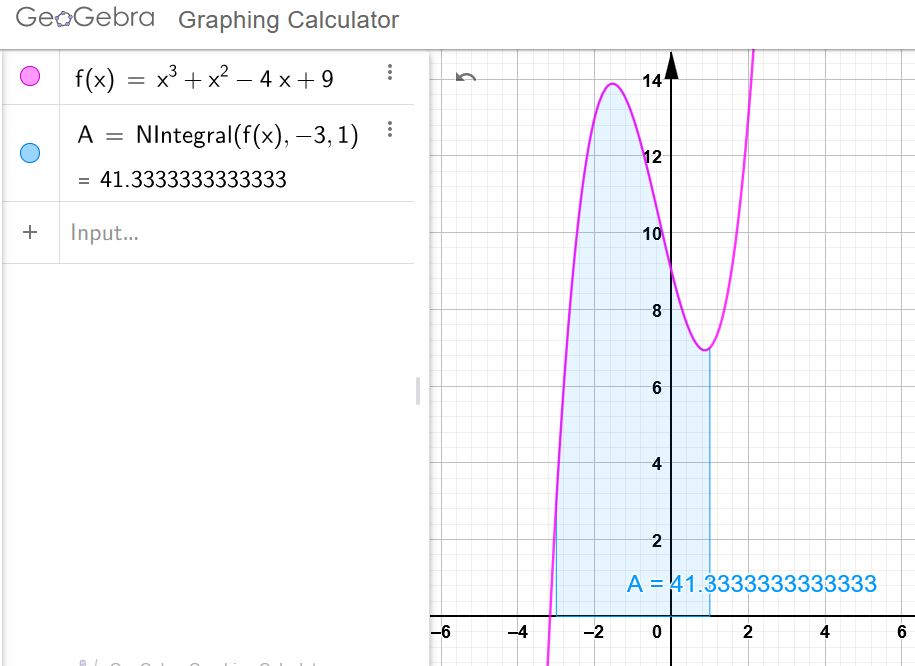
2. لإيجاد المساحة المطلوبة: اكتب في شريط الإدخال:  $Integral ( f(x), -3 , 1 )$ ، ثم اضغط (Enter)

 

3. لاحظ تظليل المنطقة وظهور قيمة التكامل على الشكل.

 

4. إذن مساحة المنطقة هي تقريبًا: 41.33 وحدة مربعة.

---

 

نهاية الدرس