الصف التوجيهي علميرياضيات فصل أول

المحل الهندسي في المستوى المركّب

العودة الى الدروس

يمكن تعريف المحل الهندسي في المستوى المركب بأنه مجموعة جميع النقاط في المستوى المركب و التي تحقق شرطاً أو شروطاً معينة،

و يمكن أن تكون هذه الشروط معادلة او متباينات.و يمكن دراسة حالات خاصة من المحل الهندسي في المستوى المركب كما يلي:

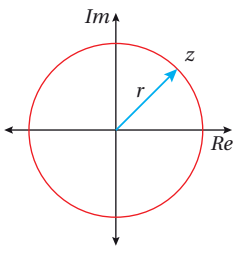
المحل الهندسي في المستوى المركب الذي تمثله المعادلة: $| z | = r, (r > 0)$

هو دائرة، مركزها نقطة الأصل $(0, 0)$ وطول نصف قطرها r .

(بعد z عن نقطة الأصل دائماً يساوي r)

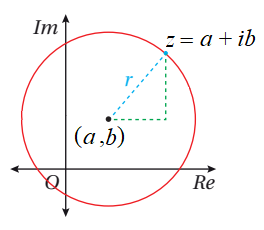المحل الهندسي في المستوى المركب الذي تمثله المعادلة: $| z - (a + i b) | = r و r > 0$

هو: دائرة، مركزها النقطة $(a, b)$ و طول نصف قطرها r

(بعد z عن (a,b) دائماً يساوي r)

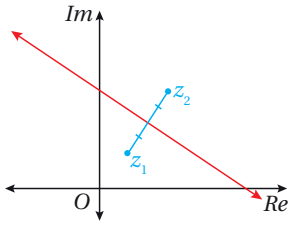
المحل الهندسي في المستوى المركب الذي تمثله المعادلة: $| z - z_{1} | = | z - z_{2} |$

هو:المنصف العمودي للقطعة المستقيمة الواصلة بين النقطتين اللتين تمثلان العددين المركبين $z_{1}, z_{2}$

(حيث بعد $Z_{2}$ عن $Z$ يساوي دائماً بعد $Z_{1}$ عن $Z$ )

فإذا كان: $z_{1} = a + i b, z_{2} = c + i d$ ، فإن المعادلة $| z - (a + i b) | = | z - (c + i d) |$

تمثل المنصف العمودي للقطعة المستقيمة الواصلة بين التقطتين $(a, b) ، (c, d)$

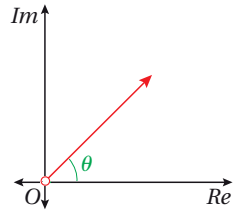
المحل الهندسي في المستوى المركب الذي تمثله المعادلة $A r g (z) = θ$ هو:

الشعاع الذي يبدأ بنقطة الأصل(ولا يحويها) و يمتد إلى مالانهاية

و يصنع زاوية قياسها $θ$ مع المحور الحقيقي الموجب حيث : $- π < θ \leq π$ .

لذلك نضع دائرة مفرغة عند نقطة الأصل لأن العدد المركب (0) سعته غير معروفة.

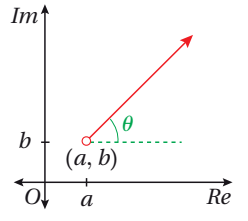المحل الهندسي في المستوى المركب الذي تمثله المعادلة: $A r g (z - (a + i b) = θ$
، حيث $- π < θ \leq π$ هو شعاع يبدأ من النقطة $(a, b)$ (ولا يحويها).

و يصنع زاوية قياسها $θ$ مع مستقيم يوازي المحور الحقيقي.

مثال:
تمثل المعادلة: $| z | = 3$ محلا هندسيا .

1) جد نوع المحل الهندسي .

الحل:

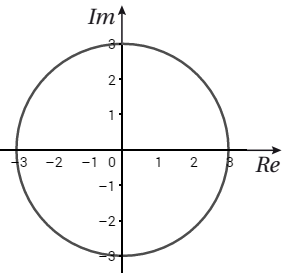
تمثل المعادلة دائرة مركزها نقطة الأصل، طول نصف قطرها 3.

2) اكتب المعادلة بالصيغة الديكارتية:

$S o l u t i o n : | z | = 3 l e t z = x + i y | x + i y | = 3 \sqrt{x^{2} + y^{2}} = 3 x^{2} + y^{2} = 9$

3) مثل المحل الهندسي في المستوى المركب

مثال:

إذا كان $| z - 3 + 2 i | = 4$

1) جد المحل الهندسي الذي تمثله المعادلة .

الحل:

المحل الهندسي هو دائرة $(3, - 2)$ ، مركزها و طول نصف قطرها 4.

لاحظ الشكل المجاور:

2) اكتب المعادلة بالصورة الديكارتية:

$S o l u t i o n : | z - (3 - 2 i) | = 4 b u t (z = x + i y) | (x - 3) + i (y + 2) | = 4 {(x - 3)}^{2} + {(y + 2)}^{2} = 16$

مثال:

جد المحل الهندسي الذي تمثله المعادلة $A r g (z + 3 - 2 i) = \frac{π}{4}$ .

الحل:

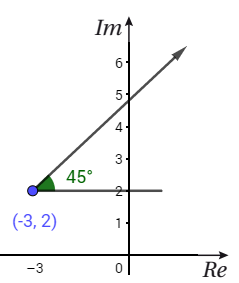
المحل الهندسي هو الشعاع الذي يبدأ من النقطة $(- 3, 2)$ ولا يحتوي هذه النقطة.

و يصنع زاوية قياسها $\frac{π}{4}$ مع المستقيم الموازي للمحور الحقيقي.

لاحظ الشكل المجاور:

مثال:

جد المحل الهندسي الذي تمثله المعادلة: $| z - 2 | = | z + 3 i |$ ثم اكتب المعادلة بالصيغة الديكارتية.

الحل:

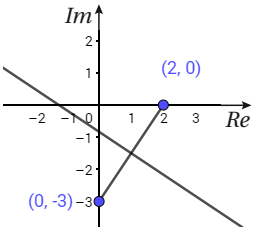
المحل الهندسي هو العمود المنصف للقطعة المستقيمة الواصلة بين النقطتين $(0, - 3), (2, 0)$ .

لاحظ الشكل المجاور:

المعادلة بالصيغة الديكارتية :

$S o l u t i o n : | (x + i y) - 2 | = | (x + i y) + 6 i | | (x - 2) + i y | = | x + i (y + 6) | \sqrt{{(x - 2)}^{2} + y^{2}} = \sqrt{x^{2} + {(y + 6)}^{2}} x^{2} - 4 x + 4 + y^{2} = x^{2} + y^{2} + 12 y + 36 - 4 x - 12 y - 32 = 0 x + 3 y + 8 = 0$

يمكن استخدام ما تعلمنا عن المحل الهندسي في المستوى المركب لتمثيل المتباينات فيه،

وذلك باستبدال رمز (=) بأحد رموز المتباينات: $(>, \geq, <, \leq)$ .

و نقوم بذلك عن طريق اتباع الخطوات التالية:

1) تحديد المنحنى الحدودي (الذي يمثل المعادلة المرافقة)

و نرسمه بخط متصل اذا احتوت المتباينة على المساواة

و بخط متقطع اذا لم تحتوي المتباينة على المساواة.

2) تحديد منطقة الحلول الممكنة: باختبار عدد مركب في احدى المنطقتين و اختباره في المتباينة.

مثال:

مثل في المستوى المركب المحل الهندسي الذي يمثل كلاً من المتباينات التالية:

$1) | z + 3 i | \leq 4$

الحل:

1) نحدد المنحنى الحدودي:
المعادلة: $| z + 3 i | = 4$ تمثل دائرة ، مركزها $(0, - 3)$ و طول نصف قطرها 4

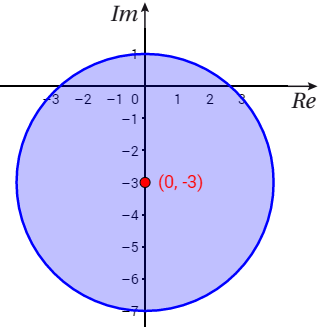
ولأن المتباينة تحتوي المساوة نرسم الدائرة بخط متصل

لاحظ الشكل التالي:

2) نحدد منطقة الحلول الممكنة:

تبعد الأعداد التي تحقق المتباينة 4 وحدات عن مركز الدائرة او اقل.

فتكون منطقة الحلول الممكنة هي: الدائرة و المنطقة الواقعة داخلها.

$2) | z + 3 | > | z - 5 i |$

الحل:

1) نحدد المنحنى الحدودي:

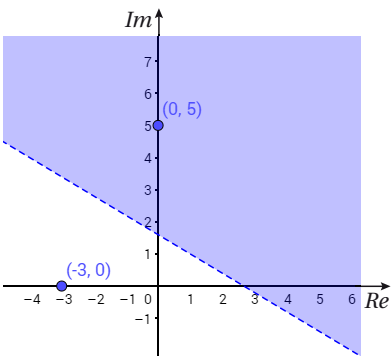المعادلة: $| z + 3 | = | z - 5 i |$ تمثل المنصف العمودي للقطعة المستقيمة الواصلة بين النقطتين $(0, 5), (- 3, 0)$ .

و يكون مستقيماً متقطعاً لعدم وجود المساواة في المتباينة.

و يمكن اختيار العدد المركب (z = 0) في المتباينة لتحديد منطقة الحلول الممكنة:

$| z + 3 | > | z - 5 i | | 0 + 3 | \overset{?}{>} | 0 - 5 i | 3 \overset{?}{>} 5 f a l s e$

إذن العدد z = 0 ، لا يحقق المتباينة، فإن منطقة الحلول الممكنة هي المنطقة التي لا تحتوي نقطة الأصل، كما في الشكل المجاور.

$3) 0 < A r g (z) \leq \frac{π}{3}$

الحل:

1. نحدد المنحنى الحدودي:

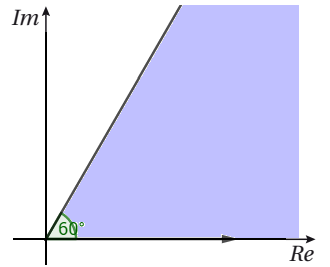المعادلة : $A r g (z) = 0$ شعاع متقطع (بسبب عدم وجود مساواة) .

يبدأ نقطة الأصل ولا يحتويها ينطبق على المحور الحقيقي الموجب.

المعادلة: $A r g (z) = \frac{π}{3}$ شعاع متصل يبدأ بنقطة الأصل و يصنع زاوية قياسها $\frac{π}{3}$ مع المحور الحقيقي الموجب.

2) يحدد منطقة الحلول الممكنة التي تمثلها المتباينة $0 < A r g (z) \leq \frac{π}{3}$ ،

و هي المنطقة المظللة المحصورة بين الشعاعين في الشكل المجاور.

$4) | z - 2 - i | \geq 2, \frac{- π}{6} < A r g (z - 2 - i) < \frac{π}{4}$

الحل:

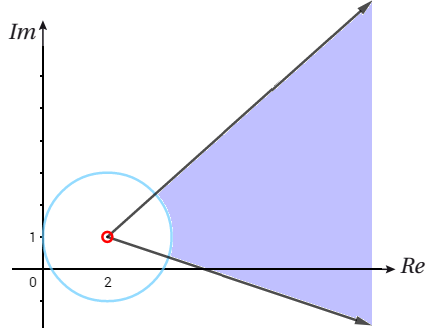
المعادلة: $| z - (2 + i) | = 2$ تمثل الدائرة ( خط متصل بسبب وجود مساواة) التي مركزها $(2, 1)$

و طول نصف قطرها 2

و المتباينة $| z - (2 + i) | \geq 6$ تمثل الدائرة السابقة و المنطقة الواقعة خارجها.

المتباينة $\frac{- π}{6} < A r g (z - (2 + i)) < \frac{π}{4}$ تمثل المنطقة المحصورة بين الشعاعين اللذين يبدءان من مركز الدائرة (ولا يحتويانها)،

الأول يصنع زاوية قياسها $\frac{- π}{6}$ مع المستقيم الموازي للمحور الحقيقي،

و الثاني يصنع زاوية قياسها $\frac{π}{4}$ معه و الشعاعان متقاطعان.

فتكون منطقة الحل الممكنة كما في الشكل التالي، الواقعة على و خارج الدائرة المحصورة بين الشعاعين.