• المتغير العشوائي: 
وهو متغير تعتمد قيمه على نواتج تجربة عشوائية .
- يرمز الى قيم المتغير العشوائي بالرمز x ، ويرمز الى المتغير العشوائي نفسه بالرمز X  .
 

- مثال (1):

في تجربة القاء قطعتي نقد عشوائياً ، إذا دل المتغير العشوائي X على عدد مرات ظهور الصورة ، فجد مجموعة قيم X .

الحل:

نفترض أن H هي الصورة ، وأن T هي الكتابة : $\Omega =(T,T),(T,H),(H,T),(H,H)$

اذن ، مجموعة قيم المتغير العشوائي هي: $X=0,1,2$

---

- مثال (2):

في تجربة إلقاء ثلاث قطع نقد متمايزة عشوائياً ، إذا دل المتغير العشوائي X  على عدد مرات ظهور الكتابة ، فجد مجموعة قيم X .
الحل:
اذن ، مجموعة قيم المتغير العشوائي هي : $X=0,1,2,3$

---

- تدريب: في تجربة إلقاء قطعة نقود 6 مرات متتالية ، إذا دل المتغير العشوائي X على عدد ظهور الصورة (H) ، فجد قيم X .

---

التوزيع الاحتمال لللمتغير العشوائي: 

التوزيع الاحتمالي للتجربة العشوائية هو اقتران يربط قيم المتغير العشوائي باحتمالات وقوعها في التجربة ، ويرمز الى اقتران التوزيع الاحتمالي بالرمز $P\left(X\right)$ ، وقد يكتب في صورة $P(X=x)$ ويمكننا التعبير عن اقتران التوزيع الاحتمالي بجدول أو تمثيل بياني. تعلم إن: مجال التوزيع الاحتمالي هو مجموعة قيم المتغير العشوائي ومداه مجموعة قيم الاحتمالات المقابلة.

 

---

مثال (3):

سحبت بطاقتان عشوائياً من وعاء يحوي البطاقات الآتية: 

إذا دل المتغير العشوائي X على مجموع العددين الظاهرين على هاتين البطاقتين ، فأنشىء جدول التوزيع الاحتمالي للمتغير X .

الحل:

$X=1,3,4,6$

---

اقتران التوزيع الاحتمالي: 

اذا كان X متغيراً عشوائياً ، فإن مجموع قيم اقتران التوزيع الاحتمالي $P(X=x)$ يساوي 1 $\sum P(X=x)=1$ حيث تساعد خاصية مجموع احتمالات قيم المتغير العشوائي على إيجاد احتمالات مجهولة في التوزيع الاحتمالي ، ثم حساب احتمالات محددة على قيم المتغير العشوائي .

- تذكر إن : المنوال هو قيمة X الاعلى تكراراً ، أي أن المنوال هو القيمة المقابلة لأعلى احتمال .

- مثال (4):

في تجربة عشوائية ، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي : 

a) جد قيمة g 
b) جد ناتج : $P(1\le X<3)$
c) جد ناتج : $P(X<4)$
d) جد منوال التوزيع.

الحل:

a) $$\begin{gathered} 0.25+g+0.35+3g=1 \\ 0.60+4g=1 \\ 4g=0.4 \\ g=1 \end{gathered}$$

b) $0.25+0.1=0.35$

c) $0.25+0.1+0.35=0.7$

d) $3$

---

- تدريب: في تجربة عشوائية ، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي : 

a) جد قيمة b
b) جد ناتج: $P(2<X\le 8)$
c) جد ناتج: $P(X\ge 2)$
d) جد منوال التوزيع.

---

• توقع المتغير العشوائي : 
- التوقع للمتغير العشوائي X في توزيع احتمالي لتجربة عشوائية يساوي مجموع حواصل ضرب كل قيمة للمتغير X في احتمال تلك القيمة .

- مثال (5): تجد حنين عددًا من الرسائل في بريدها الإلكتروني كل يوم، فقررت رصد عدد الرسائل التي وصلتها يوميا من 50 يوما اختيرت عشوائيا، وكانت النتائج التي توصلت إليها كما في الجدول الآتي:

بافتراض أن المتغير العشوائي X يمثل عدد الرسائل اليومية التي تصل البريد الالكتروني لحنين : 
1) أنشىء جدول التوزيع الاحتمالي للمتغير العشوائي X
2) جد توقع المتغير العشوائي X .

الحل:

1)

2) $E\left(X\right)=\frac{119}{50}=2.38$

---

-  تدريب : جد القيمة المتوقعة للتوزيع الاحتمال الآتي : 

---

مثال (6) :

يحتوي وعاء على 6 بطاقات حمراء، و 4 بطاقات زرقاء، جميعها متماثلة. إذا سحبت منها بطاقتان على التوالي من دون إرجاع، ودل المتغير العشوائي X على عدد البطاقات الزرقاء المسحوبة، فأجد E(X) .

الحل:

$E\left(X\right)=(0\times \frac{1}{3})+(1\times \frac{24}{45})+(2\times \frac{2}{15})=0.8$

---

تباين المتغير العشوائي : 

- وهو مقياس لتشتت قيم المتغير عن وسطها الحسابي E(X) ، ويرمز إليه بالرمز Var(X)  - التباين للمتغير العشوائي X في توزيع احتمالي لتجربة عشوائية يساوي مجموع نواتج ضرب مربعات قيم المتغير X في احتمال كل قيمة ، مطروحاً منه مربع توقع المتغير X . $Var\left(X\right)={\sigma }^2=\sum (x^2.P(x\left)\right)-\left(E\right(X){)}^2$

---

- مثال (7): يبين الجدول الآتي التوزيع الاحتمالي للمتغير العشوائي X .

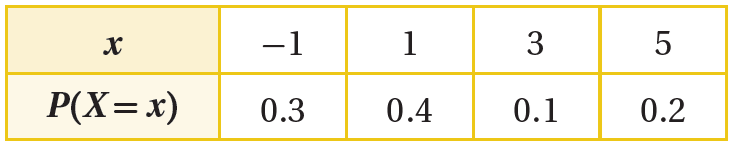
a) جد التوقع $E\left(X\right)$                        

b) جد التباين $Var\left(X\right)$

الحل:

a) $E\left(X\right)=\sum x.P\left(x\right)$

$E\left(X\right)=(-1\times 0.3)+(1\times 0.4)+(3\times 0.1)+(5\times 0.2)=1.4$

b) $Var\left(X\right)=\sum (x^2.P(x\left)\right)-\left(E\right(X){)}^2$

$Var\left(X\right)=(1\times 0.3)+(1\times 0.4)+(9\times 0.1)+(25\times 0.2)-(1.4{)}^2=0.14$

---