• نتاجات الدرس:
- تحديد النقاط الحرجة ، وفترات التزايد والتناقص لاقترانات كثيرات الحدود .
- تصنيف النقاط الحرجة لاقترانات كثيرات الحدود باستعمال المشتقة .
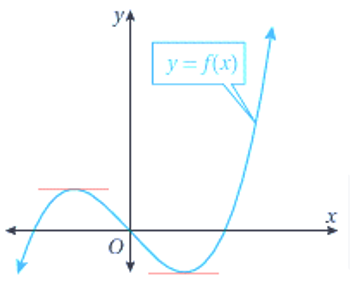 |
النقاط الحرجة للاقتران: توجد على منحنى الاقتران f(x) المبين جانباً نقطة واحدة على الأقل يمكن رسم مماس أفقي عندها، في ما يُعرف بالنقطة الحرجة وهذا يعني أن مشتقة الاقتران عند هذه النقطة تساوي صفراً، ويُسمّى الإحداثي x للنقطة الحرجة ، قيمة حرجة. |
- مثال (1): جد النقاط الحرجة لكل اقتران مما يأتي :
1) 2)
الإجابة:
1)
اذن ، توجد نقطة حرجة للاقتران f عندما x=1
أما النقطة الحرجة هي:
2)
اذن ، توجد نقطة حرجة للاقتران f عندما x=1,x=2
أما النقطة الحرجة هي:
- تدريب : جد النقاط الحرجة لكل اقتران مما يأتي :
1) 2)
التزايد والتناقص للاقترانات كثيرات الحدود :
يكون الاقتران متناقصاً في الفترة المفتوحة إذا كان لكل في الفترة .
يكون الاقتران متزايداً في الفترة المفتوحة إذا كان لكل في الفترة .
| نظرية: إذا كان لقيم جميعها في الفترة المفتوحة ، فإن الاقتران يكون متزايداً على الفترة . إذا كان لقيم جميعها في الفترة المفتوحة ، فإن الاقتران يكون متناقصاً على الفترة . |
• خطوات الحل:
1) نجد مشتقة الاقتران ، ثم نجد أصفار المشتقة.
2) نبحث في أشارة المشتقة باستعمال خط الأعداد.
3) نحدد فترات التزايد والتناقص.
• مثال (2) : حدد فترات التزايد والتناقص لكل اقتران في ما يأتي:
a)
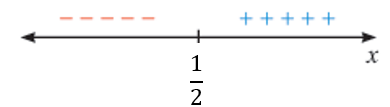
متزايد في الفترة ومتناقص في الفترة .
b)
- اذن: المميز أقل من صفر
اذن h(x) متزايد دائماً ( متزايد على )
c)

اذن، متزايد في الفترة والفترة ومتناقص في الفترة
- تدريب: حدد فترات التزايد والتناقص لكل اقتران مما يأتي :
1) 2)
• تصنيف النقاط الحرجة لاقترانات كثيرات الحدود باستعمال المشتقة .
حيث يمكن استعمال المشتقة ، لتصنيف النقاط الحرجة لاقترانات كثيرات الحدود :
1) نقطة عظمى محلية
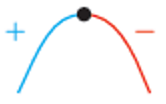 |
النقطة الحرجة التي يكون منحنى الاقتران عن يسارها متزايدًا وعن يمينها متناقصاً، ما يعني أن إشارة المشتقة ، عند الحركة من يسار النقطة إلى يمينها تتغير من الموجب إلى السالب . |
2) نقطة صغرى محلية
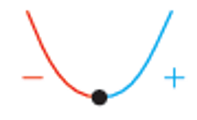 |
النقطة الحرجة التي يكون منحنى الاقتران عن يسارها متناقصاً وعن يمينها متزايدًا، ما يعني أن إشارة المشتقة عند الحركة من يسار النقطة إلى يمينها تتغير من السالب إلى الموجب . |
3) نقطة انعطاف أفقي
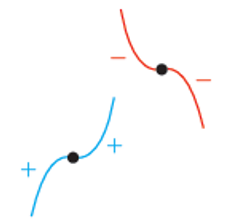 |
النقطة الحرجة التي يكون منحنى الاقتران حولها إما متزايدًا وإما متناقصاً، ما يعني عدم تغير إشارة المشتقة عند الحركة من يسار النقطة إلى يمينها، بل تبقى كما هي إما موجبة وإما سالبة. |
أتعلم:
• القيمة العظمى المحلية هي الإحداثي y للنقطة العظمى المحلية، وتسمى كذلك؛ لأنها أكبر من القيم المحاورة لها.
• القيمة الصغرى المحلية هي الإحداثي y للنقطة الصغرى المحلية، وتسمى كذلك؛ لأنها أصغر من القيم المجاورة لها.
مثال (3): إذا كان الاقتران ، فأستعمل المشتقة لحل السؤالين الآتيين :
1) جد النقاط الحرجة للاقتران f(x)
2) صنف النقاط الحرجة الى عظمى محلية أو صغرى محلية أو انعطاف أفقي .
الاجابة :
1)
النقطة الحرجة:
النقطة الحرجة:
2)
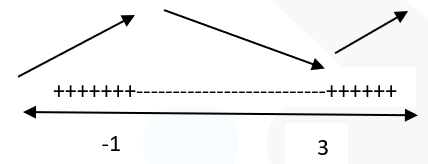
يوجد قيمة عظمى محلية عند النقطة وصغرى محلية عند
- تدريب: جد النقاط الحرجة للاقتران الآتي ، ثم حدد نوعها باستعمال المشتقة .
• يمكن نمذجة كثير من المواقف الحياتية والعلمية باقترانات كثيرات الحدود ، وعندئذ يستفاد من تحديد تزايد تلك الاقترانات وتناقصها وقيمها العظمى والصغرى في تحليل تلك المواقف وتفسيرها .
مثال (4): لاحظ عالم حيوانات أن عدد الضفادع في بحيرة ما يمكن نمذجته بالاقتران: ، حيث P عدد الضفادع ، و t الزمن بالأشهر منذ بدء ملاحظة الضفادع . جد أكبر عدد يمكن أن تصل إليه الضفادع في البحيرة منذ بدء ملاحظتها.
الإجابة:
النقطة الحرجة:
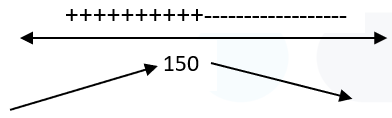
يوجد قيمة عظمى محلية للاقترانp(t)
(عدد الضفادع) عندما t=150 هو 10000
- تدريب: تنتج إحدى الشركات صناديق لتخزين البضائع على شكل متوازي مستطيلات. إذا أمكن نمذجة حجم كل من هذه الصناديق بالاقتران: ، فأجد قيمة x التي تجعل حجم الصندوق أكبر ما يمكن.