الاقترانات المتشعبة

الاقترانات المتشعبة

فكرة الدرس: تعرف الاقتران المتشعب واقتران القيمة المطلقة وتمثيلهما بيانيًا وتحديد مجال كل منهما ومداه

بعض المسائل الحياتية لا يمكن التعبير عنها باستخدام اقتران بدلالة قاعدة واحدة كما الحال في حساب قيمة فاتورة الكهرباء حسب الشرائح وتعرفة كل منها، لذا نحتاج إلى معادلة خاصة لكل واحدة من شرائح الاستهلاك وهنا سنستخدم اقترانا خاصا يسمى اقترانًا متشعبًا.

الاقتران المتشعب: هو اقتران معرف بقواعد مختلفة عند أجزاء مجاله.

في هذا الدرس سنتعرف على الاقتران المتشعب مجاله ومداه وتمثيله بيانيا وكذلك الحال على الاقتران المطلق.

مثال:

 إذا كان :

$f\left(x\right)=\left\{\begin{array}{ll}3x-1& ,-1\le x<2\\ x^3& ,x\ge 2\end{array}\right.$ 

1) أحدد مجال f(x).

الاقتران f(x) معرف على قاعدتين مجال القاعدة الأولى هو الفترة $[-1,2)$، والقاعدة الثانية معرفة على الفترة $[2,\infty )$، إذن مجال الاقتران f(x) هو الفترة $[-1,\infty )$

2) أجد قيمة f(0) ,و f(2).

بما أن $-1<0<2$ إذن نستعمل القاعدة

 $$\begin{gathered} f\left(x\right)=3x-1 \\ f\left(0\right)=3\times 0-1 \\ =-1 \end{gathered}$$

بما أن $2\ge 2$ إذن نستعمل القاعدة 

$$\begin{gathered} f\left(x\right)=x^3 \\ f\left(2\right)=2^3 \\ =8 \end{gathered}$$

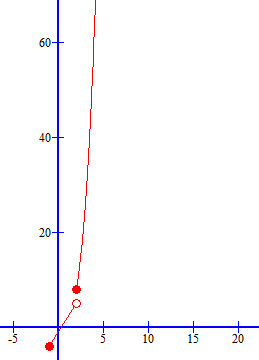
3) أمثل الاقتران بيانيا وأحدد مداه.

أولا: نمثل القاعدة الأولى $f\left(x\right)=3x-1$ عندما $-1\le x<2$

نجد قيمة الاقتران f(x) عندما x= - 1 , x= 2 كما في الجدول

مع مراعاة ان هذا الفرع من الاقتران ليس معرف عند طرف الفترة(2) لذا عند التمثيل لهذا الفرع نضع دائرة مفتوحة

X	-1	2
y=f(x)=3x-1	-4	5
(x,y)	(-1,-4)	(2,5)

ثانيا: نمثل القاعدة الثانية $f\left(x\right)=x^3$ عندما $x\ge 2$

نجد قيمة الاقتران f(x) عندما $x=2$ وقيمتين أكبر منها كما في الجدول

X	2	3	4
$y=f\left(x\right)=x^3$	8	27	64
(x , y)	(2 , 8)	(3 , 27)	(4 , 64)

من خلال الرسم نلاحظ أن مدى الاقتران هو $y\ge -4$ ويمكن التعبير عنه بالفترة $[-4,\infty )$

ملاحظة: إذا كان لدينا تمثيل بياني لاقتران متشعب يمكننا إيجاد قاعدة ذلك الاقتران من خلال التمثيل البياني له.

مثال:

أكتب قاعدة الاقتران f(x) الممثل بيانيا في الشكل المجاور.

 

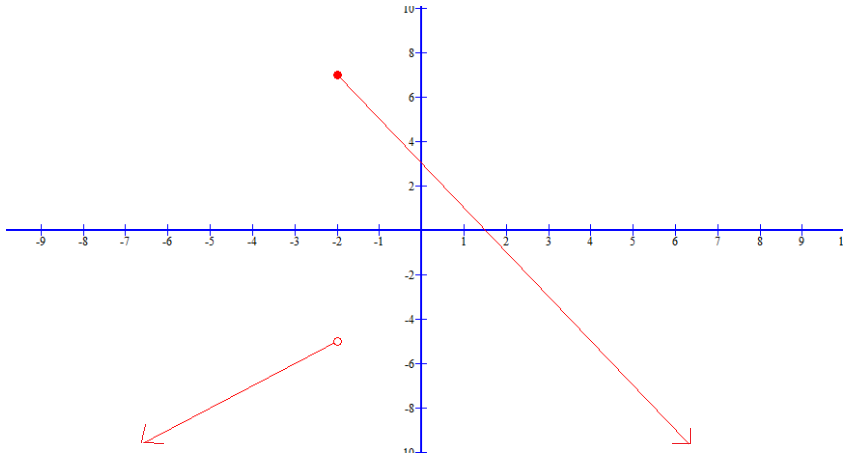
أولا: نكتب قاعدة الجزء الأيسر من الرسم وهو عبارة عن اقتران خطي ميله = 1 ويمر بالنقطة $(-3,-6)$ فتكون القاعدة هي $f\left(x\right)=x-3$ ووجود دائرة مفتوحة عند النقطة $(-2,-5)$ يعني أن هذه القاعدة تقابل الفترة $(-\infty ,-2)$.

ثانيا: نكتب القاعدة التي تمثل الجزء الأيمن من الرسم وهو عبارة عن اقتران خطي مقطع الصادي y = 3 وميله = 2- فتكون القاعدة هي $f\left(x\right)=-2x+3$ ووجود دائرة مظللة عند النقطة $(-2,7)$ يعني أن هذه النقطة تقابل الفترة $[-2,\infty )$.

ثالثا: نكتب قاعدة القتران المتشعب

$f\left(x\right)=\left\{\begin{array}{l}x-3 , x<-2\\ -2x+3 , x\ge -2\end{array}\right.$

اقتران القيمة المطلقة

اقتران القيمة المطلقة هو اقتران يحتوي على قيمة مطلقة لمقدار جبري ومن أبسط الأمثلة عليه $f\left(x\right)=\left|x\right|$ ويمكن كتابته بصورة اقتران متشعب كما يأتي:

$f\left(x\right)=\left|x\right|=\left\{\begin{array}{ll}-x& , x<0\\ x& , x\ge 0\end{array}\right.$

ملاحظة:إعادة تعريف اقتران القيمة المطلقة تعني كتابة أي اقتران قيمة مطلقة على صورة اقتران متشعب من دون استعمال رمز القيمة المطلقة.

مثال:

أعيد تعريف كل من الاقترانات الآتية:

$1) f(x)=\left|3x-6\right|$

أولاً:  نساوي ما داخل المطلق بالصفر  ونحل المعادلة الناتجة

$$\begin{gathered} 3x-6=0 \\ x=2 \end{gathered}$$

ثانياً: نعين صفر المعادلة على خط الأعداد ونحدد الإشارة على جانبيه، ويتم ذلك بتعويض قيمتين

1)واحدة أكبر من 2 (تقع على يمين 2)فيكون الناتج موجباً مما يعني أن الإشارة على يمين 2 موجبة على خط الأعداد دائماً

2)قيمة أخرى أقل من 2(تقع على يسار 2) فيكون الناتج سالباً مما يعني أن الإشارة على يسار 2 سالبة على خط الأعداد دائماً

 

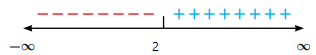
ثالثاً: نكتب قاعدتي الاقتران حسب إشارة يمين صفر المعادلة ويساره

$f\left(x\right)=\left\{\begin{array}{l}-(3x-6) , x<2\\ (3x-6) , x\ge 2\end{array}\right.$

$2) f(x)=\left|x^2-x-6\right|$

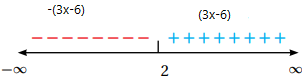
نتبع خطوات المثال السابق من مساواة ما داخل المطلق بالصفر وإيجاد أصفار المعادلة واختبارها على خط الأعداد.

$$\begin{gathered} x^2-x-6=0 \\ (x-3) (x+2)=0 \\ x=3 , x=-2 \end{gathered}$$

$f\left(x\right)=\left\{\begin{array}{l}{x}^2-x-6 , x\le -2 , x\ge 3\\ -x^2+x+6 , -2<x<3\end{array}\right.$

 

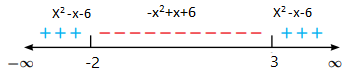
مثال:

أجرة ساعة العمل الواحدة في إحدى الشركات 4 دنانير خلال أوقات العمل النظامية المعتادة ضمن 40 ساعة عمل في الاسبوع. وتدفع الشركة لكل ساعة عمل إضافي فوق ذلك أجرة الساعة ونصف من ساعات العمل المعتاد. أكتب اقترانا لحساب الأجرة الأسبوعية لعامل اشتغل x ساعة في أسبوع.

يوجد في المسألة قاعدتان لحساب الأجرة؛ تبعا لعدد ساعات العمل.

عدد الساعات	الأجرة
$0\le x\le 40$	4x
$x>40$	4(40)+6(x-40)

إذن: اقتران الأجرة هو:

$f\left(x\right)=\left\{\begin{array}{l}4x , 0\le x\le 40\\ 6x-80 , x>40\end{array}\right.$

تمثيل اقتران القيمة المطلقة بيانيا:

الاقتران $f\left(x\right)=a\left|mx+b\right|+c$ حيث $m\ne 0 , a\ne 0$ يمكن تمثيله بيانيا حيث يتكون من شعاعين على شكل حرف V متماثلين حول المحور $x=-\frac{b}{m}$ ورأس الاقتران (النقطة التي يصل عندها إلى أعلى قيمة أو أقل قيمة) تكون إحداثياتها $\left(\frac{-b}{m} , c\right)$.

مثال:

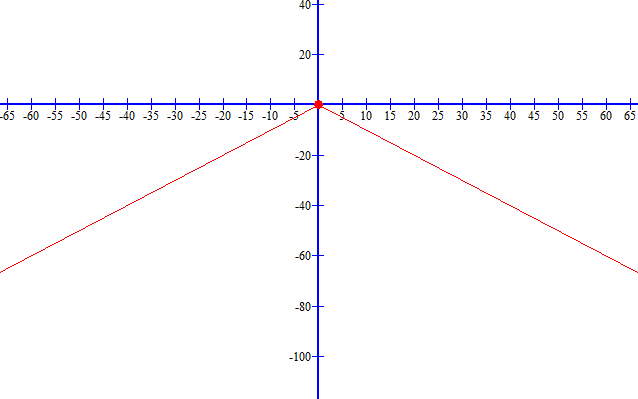
أمثل بيانيا كل مما يأتي محددا مجاله ومداه.

$1) f(x)=\left|-x\right|$

أولا: نجد أحداثي نقطة رأس الاقتران، ومعادلة محور التماثل.

نجد أحداثي نقطة الرأس.

$$\begin{gathered} b=0 , m=-1 , c=0 , a=1 \\ (\frac{-b}{m},c) \\ =(0,0) \end{gathered}$$

ثانيا: أحدد قيمتين للمتغير x حول محور التماثل، ثم أجد صورتيهما.

بما أن محور التماثل x=0 ، أختار قيمة للمتغير x أكبر من 0  (مثلا 1) وقيمة أخرى أقل من 0 (مثلا 1-)، ثم أجد صورتيهما في الاقتران.

1	1-	x
1	1	$f\left(x\right)=\left|-x\right|$
$(1,1)$	$(-1,1)$	$(x,y)$

ثالثا: أمثل النقطتين في المستوى الإحداثي، وأصل بين النقاط الثلاثة بشكل V.

$2) f(x)=2-\left|x+1\right|$

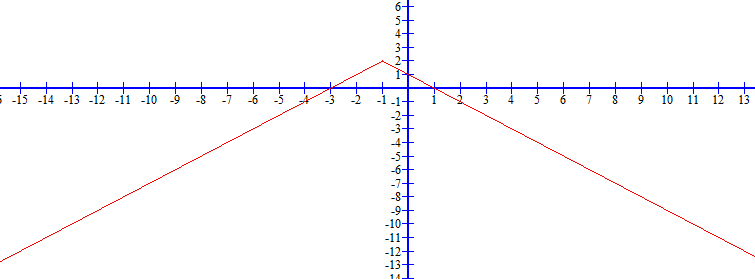
أولا: نجد أحداثي نقطة رأس الاقتران، ومعادلة محور التماثل.

نجد أحداثي نقطة الرأس.

$$\begin{gathered} a=-1 , b=1 , c=2 , m=1 \\ (\frac{-b}{m},c) \\ =(\frac{-1}{1},2)=(-1,2) \end{gathered}$$

ثانيا: أحدد قيمتين للمتغير x حول محور التماثل، ثم أجد صورتيهما.

بما أن محور التماثل x=-1 ، أختار قيمة للمتغير x أكبر من 1-  (مثلا 0) وقيمة أخرى أقل من 1- (مثلا 2-)، ثم أجد صورتيهما في الاقتران.

x	2-	0
$f\left(x\right)=2-\left|x+1\right|$	1	1
$(x,y)$	$(-2,1)$	$\left(0,1\right)$

ثالثا: أمثل النقطتين في المستوى الإحداثي، وأصل بين النقاط الثلاثة بشكل V.

ملاحظة: يمكننا إيجاد قاعدة اقتران القيمة المطلقة لمقدار خطي إذا أعطي تمثيله البياني.

مثال:

أكتب قاعدة الاقتران f(x) الممثل بيانيا في الشكل المجاور.

 

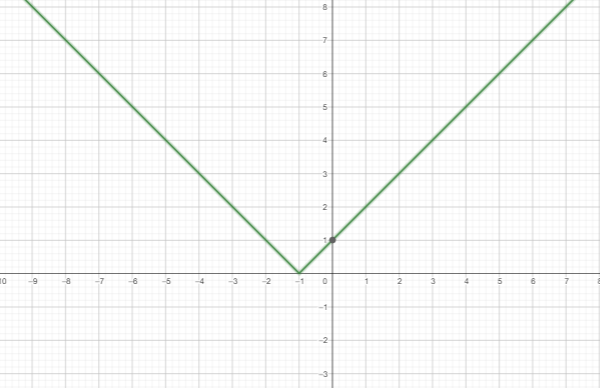
أولا: نجد ميل المعادلة الخطية داخل رمز المطلق.

الشعاع الأيمن يمر بالنقطتين $(-1,0) ، (0,1)$ إذن الميل= $m=\frac{y_2-y_1}{x_2-x_1}=\frac{0-1}{-1-0}=1$.

ثانيا: نجد أحداثي نقطة الرأس ونعوض الميل ونقطة الرأس في قاعدة الاقتران

$$\begin{gathered} x=\frac{-b}{m} \\ -1=\frac{-b}{1} \\ b=1 \end{gathered}$$

الصورة العامة لقاعدة الاقتران المطلق $f\left(x\right)=a\left|mx+b\right|+c$ وبالتالي تكون $f\left(x\right)=a\left|x+1\right|+0$

والآن نجد قيمة a من خلال تعويض أي نقطة تقع على منحنى الاقتران مثل $(1,2)$

$$\begin{gathered} f\left(x\right)=a\left|x+1\right| \\ 2=a\left|1+1\right| \\ 2=2a \\ a=1 \\ f\left(x\right)=\left|x+1\right| \end{gathered}$$