الاشتقاق

الاشتقاق

تعرفنا في الدرس السابق على كيفية إيجاد الميل أو تقديره وهي بالطريقة ليست سهلة وتحتاج إلى دقة عند رسم المماس لذا سنتعرف في هذا الدرس على طريقة جبرية أسهل لإيجاد ميل منحنى الاقتران عند نقطة معينة واقعة عليه دون الحاجة للرسم البياني.

---

• عند إيجاد ميل منحنى الاقتران y = x² عند نقاط مختلفة عليه باستعمال طريقة ميل المماس التي تناولناها في الدرس السابق نلاحظ أن ميل المنحنى عند أي نقطة (x, y) يساوي قيمة x مضروبةً في العدد 2 أي أنو الميل يساوي 2x. 

وبوجه عام فإن ميل منحنى f(x) = xⁿ   عند أي نقطة (x, y)  هو $m = n x^{n-1 }$  وهي مشتقة الاقتران f (x) عند نقطة واقعة عليه ويرمز لها بالرمز $f\text{'}\left(x\right)$

مفهوم أساسي

مشتقة اقتران القوة 

• بالكلمات : عند اشتقاق الاقتران f(x) = xⁿ فإن أس x  في المشتقة يكون أقل بواحد من أس x  في الاقتران الأصلي وأن معامل x  في الشتقة يساوي أس x  في الاقتران الأصلي 
• بالرموز : إذا كان f(x) = xⁿ  حيث n  عدد صحيح غير سالب فإن $f^{\text{'}}\left(x\right) = n x^{n-1}$

مثال 

أجد المشتقة لكل من ما يأتي 

1. f(x) = x⁵

f ' (x) = 5 x^{5 - 1} = 5 x⁴

 

2. f(x) = x¹³

f ' (x) = 13 x¹²

---

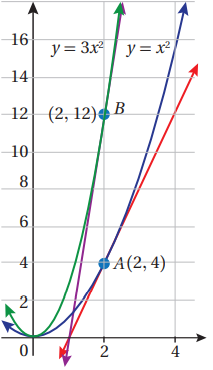
• من المعلوم أن قيم y  للاقتران f(x) = 3x²   تساوي 3 أمثال قيم y  التي تناظرها للاقتران g(x) = x² ، وعليه فإن ميل منحنى الاقتران f(x) عند النقطة ( 12 , 2)  يساوي 3 أمثال ميل منحنى الاقتران g(x) عند النقطة ( 4 ,2 )  وهذا يعني أن مشتقة  3x ² تساوي 3 أمثال مشتقة x²

 

^{مفهوم أساسي :}

قواعد أخرى للمشتقة :

1. مشتقة مضاعفات القوى : 

إذا كانت f(x) = ax ⁿ  حيث n  عدد صحيح غير سالب فإن f '(x) = an x^{n -1}  

2. مشتقة الثابت :

إذا كانت f(x) = c   حيث c  عدد حقيقي  فإن f '(x) = 0   

---

مثال 

أجد f'(x)  لكل مما يأتي 

1.  f(x) = -3 x⁷

f ' (x) = -3 (7) x ^{7 - 1}  = -21 x ⁶

2. f(x) = 5 x²

f '(x) = 5 (2) x ^{2- 1} = 10 x

3. f(x) = -10

f '(x) = 0

---

مفهوم أساسي 

مشتقة المجموع و مشتقة الفرق :

• بالكلمات مشتقة مجموع كثيري الحدود تساوي مجموع مشتقتيهما 

ومشتقة الفرق بين كثيري الحدود تساوي الفرق بين مشتقتيهما 

• بالرموز  إذا كان $f\left(x\right) = g\left(x\right) \pm h\left(x\right)$ حيث g(x) و h(x)  كثيرا حدود فإن $f \text{'} \left(x\right) = g\text{'}\left(x\right) \pm h\text{'}\left(x\right)$

مثال 

أجد مشتقة كل مما يأتي 

1.  $$\begin{gathered} f\left(x\right) = x^3 + 3x \\ \mathbf{ }\mathit{f}\mathbf{\text{'}}\mathbf{ }\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{3}{\mathit{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{3}\mathbf{ } \end{gathered}$$

 

$$\begin{gathered} 2. f\left(x\right) = \frac{1 }{5} x^5 + 3 x^4 - 6 \\ \mathit{f}\mathbf{\text{'}}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{1}}{\mathbf{5}}\mathbf{ }\mathbf{\left(}\mathbf{5}\mathbf{\right)}\mathbf{ }{\mathit{x}}^{\mathbf{4}}\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{3}\mathbf{ }\mathbf{\left(}\mathbf{4}\mathbf{\right)}\mathbf{ }\mathbf{ }{\mathit{x}}^{\mathbf{3}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{0}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{4}}\mathbf{ }\mathbf{+}\mathbf{12}\mathbf{ }{\mathit{x}}^{\mathbf{3}} \end{gathered}$$

---

• نلاحظ من الأمثلة السابقة أن مشتقة الاقتران هي اقتران جديد يمثل قيمة ميل منحنى الاقتران الأصلي عند قيم مختلفة وبالتالي يمكن إيجاد ميل منحنى الاقتران عند أي نقطة عليه وذلك بتعويض الإحداثي x لتلك النقطة في اقتران المشتقة 

( المشتقة عند نقطة معينة  وإيجاد الميل باستخدام المشتقة )

مثال 

إذا كان f(x) = 2x ³ -10 x + 1  ، استعمل المشتقة لإيجاد ميل المنحنى f(x) عند النقطة ( 7 - , 1) 

f(x) = 2 x³ -10 x +1

f'(x) = 6x²  -10 

f '(1) =  -4 

ميل منحنى الاقتران f(x)  عند النقطة ( 7 - , 1 ) يساوي 4 - 

---

• تعرفنا في الدرس السابق أن ميل منحنى المسافة - الزمن في لحظة ما يساوي السرعة اللحظية عند تلك النقطة و بصورة مشابهة فإن ميل منحنى السرعة - الزمن في لحظة ما يساوي التسارع اللحظي فنستطيع إيجاد كل من السرعة اللحظية و التسارع اللحظي باستعمال المشتقى بسهولة دون الحاجة لتقدير ميل المنحنى باستعمال المماس كما في الدرس السابق .

مثال من الحياة 

يمثل الاقتران d(t) = 1.2 t²  - 5 t +4 المسافة (بالمتر) التي يقطعها جسيم متحرك حيث أن t هو الزمن بالثانية أجد

1. سرعة الجسيم بعد 2 ثانية من بدء الحركة 

2. تسارع الجسيم بعد 4 ثواني من بدء الحركة 

d (t) =  1.2 t²  - 5t + 4

v(t) = d'(t) = 2.4 t -5

a (t) = v'(t) = 2.4

1. v(2) = 4.8 +5 = 9.8

2. a (4) = 2.4 

---