فكرةُ الدَّرس: أَحسبُ مِساحةَ مُتوازي الأضلاع، وأحلّ مَسائلَ عليها.
المُصطلحات: القاعدةُ، الارتفاعُ.
|
تعلَّمْتُ سابقا أَنَّ مُتوازِيَ الأضْلاعِ مُضلّعٌ رُباعِي فيهِ كلّ ضِلعين مُتقابِلَينِ مُتَساويانِ في الطّولِ وَمُتوازيانِ.
|
 |
مَفهومٌ أَساسيٌّ: مِساحةُ مُتوازي الأضلاعِ
|
بِالكَلِمات: مِساحةُ مُتَوازي الأضلاع هِي حاصِلُ ضَرب طول القاعدَة في الارتفاع. بالرُّموزِ:
|
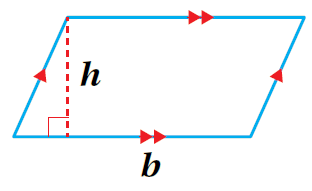 |
مثال
أجدُ مساحة مُتوازي الأضلاع في كُلّ ممّا يأتي:
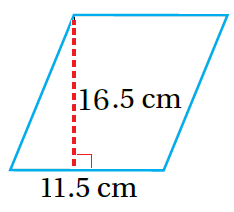 |
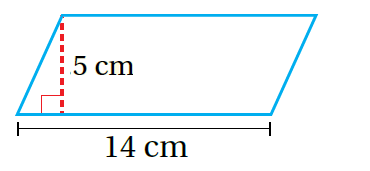 |
| صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ | صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ |
يُرسمُ مُتوازي الأضلاع أحيانًا على شبكة المُربّعات، ويُمكنُ عندئذٍ تحديدُ طول قاعدته وارتفاعه بعدّ المُربّعات، وتكونُ المساحةُ بالوحدة المُربّعة.
مثال
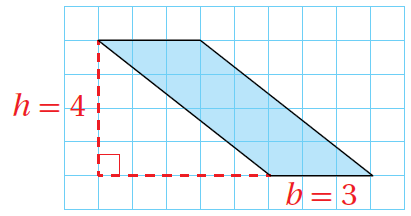
أحسُبُ مساحة مُتوازي الأضلاع في الشّبكة الآتية:
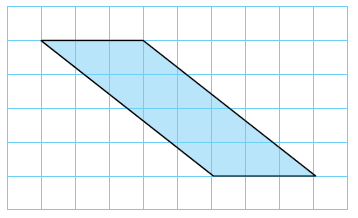 |
الجواب
أعُدُّ الوحدات الأفُقيّة لأجد طول قاعدة مُتوازي الأضلاع، ثُمّ أعُدُّ الوحدات الرّأسيّة لأجد ارتفاعهُ. أُلاحظُ أنّ b تُساوي 3 وحدات و h تُساوي 4 وحدات.
 |
| صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ |
تعلمتُ سابِقًا أن الشكل المُركب شكلٌ ناتِجٌ عن تركيبِ شكلينِ هندسِيينِ أو أكثر، ويُمكِنُ حِسابُ مِساحتهِ بِاستِعمالِ مِساحاتِ الأشكالِ المُكونةِ لهُ التي يُمكِنُ أن يكون أحدُها مُتوازِي أضلاع.
مثال
أجدُ مساحة الْمنْطقة الْمُظللة في كُل مما يأْتي:
1)

المنطقةُ المُظللةُ هي مُربعٌ ومُتوازي أضلاعٍ . أجدُ مساحة المنطقة المُظللة بجمع مِساحَةِ مُتَوازي الَْضْلاعِ A1 إِلى مِساحَةِ الْمُرَبَّعِ A2
| صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ هي |
| صيغَةُ مِساحَةِ المُربع الذي طول ضلعه s هي |
| أَجْمَعُ الْمِساحَتَيْنِ: |
2)
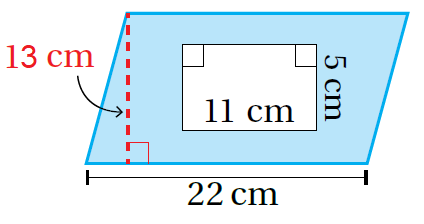
المنطقةُ المُظلّلةُ هي مُتوازي أضلاعٍ مُفرغٌ منهُ مُستطيلٌ. أجدُ مساحة الشّكل بطرح مساحة المُستطيل A2 من مساحة مُتوازي الأضلاع A1
| صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ هي |
| صيغَةُ مِساحَةِ الْمُسْتَطيلِ هي |
| أَطْرَحُ الْمِساحَةَ الصُّغْرى مِنَ الْمِساحَةِ الْكُبْرى |
يُمكِنُ استعمالُ صيغة مساحَة مُتوازي الأضلاعِ في كَثير مِنَ المواقفِ الحياتِية.
|
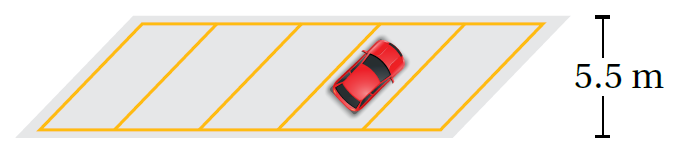
مثال تَظهَرُ في الشَّكل المُجاورِ ساحةُ اصطفافٍ 110 m2 عَلى شَكل مُتَوازي أَضلاع مساحَتُه وَارتِفاعُه 5.5 m ، أَجدُ طولَ قاعدَة مِساحَةِ الاصطِفافِ. |
 |
الجواب
| صيغَةُ مِساحَةِ مُتَوازي الأضْلاعِ هي |