لحل نظام يتكون من معادلتين تربيعيتين،نساوى أو لا المعادلتان بعضهما ببعض لتكوين معادلة تربيعية واحدة
مثال:
أحل نظام المعادلات الآتي، ثم أتحقق من صحة الحل:
عند تمثيل معادلتي النظام على المستوى الإحداثي نفسه، يلاحظ أن منحنييهما يتقاطعان في نقطتين كما في الشكل المجاور؛ ما يعني أن للنظام حلين مختلفين. أتحقق من ذلك جبريا. بداية، يجب مساواة معادلتي النظام المعطى، ثم حل المعادلة التربيعية الناتجة:
مساواة المعادلتين ثم تجميع الحدود
أحل المعادلة التربيعية الناتجة باستعمال التحليل:
تحليل المعادلة التربيعية الناتجة وايجاد الحلول
لإيجاد قيمة y، أعوض قيمتي x في أي من معادلتي النظام:
الحالة الأولى: إذا كانت x=0:
إذن،الحل الأول للمعادلة هو:
الحالة الثانية: إذا كانت x=-1:
إذن، الحل الثاني للمعادلة هو:
إذن، حل النظام هو:
قد يتقاطع منحنيا معادلتين تربيعيتين في نقطة واحدة فقط، وعندئذ يكون لنظام المعادلات الذي تكونه هاتان المعادلتان حل واحد
مثال: من الحياة
سباقات: في أحد سباقات المراحل، سلك متسابق مسارا تمثله المعادلة التربيعية: في حين سلك متسابق آخر مسارا تمثله المعادلة: . اجد نقطة التقاطع بين مساري المتسابقين
اكتب المعادلة بالصورة القياسية (بدلالة y)
عند تمثيل المعادلتين بيانيا كما في الشكل المجاور، يلاحظ وجود نقطة تقاطع واحدة بين منحنييهما؛ ما يعنى ان لنظام المعادلات حلا واحدا. اتحقق من ذلك جبريا
بداية، يجب مساواة معادلتي النظام المهطى، ثم حل المعادلة التربيعية الناتجة:
بعد ذلك اجد قيمة y، وذلك بتعويض قيمة في اي من معادلتي النظام:
ذان، حل نظام المعادلات هو: ، ونقطة تقاطع المنحنيين هي:
عرضنا في المثالين السابقين انظمة معادلات تربيعية لها حلان او حل واحد. ولكن، هل يوجد دائما حل للنظام المكون من معادلتين تربيعيتين؟ ادرس المثال الاتي
مثال
احل نظام المعادلات الاتي:
عند تمثيل المعادلتين بيانيا كما في الشكل المجاور، يلاحظ عدم وجود نقاط تقاطع ىبين منحنييهما؛ ما يعني عدم وجود حل لنظام المعادلات. اتحقق من ذلك جبريا.
بداية، يجب مساواة معادلتي النظام المعطى، ثم حل المعادلة التربيعية الناتجة لايجاد قيمة x:
بعد ذلك اجد قيمة المميز لتحديد اذا كان للمعادلة التربيعية الناتجة حل او لا.
قيم المعاملات هي: . وبالتعويض في المميز ينتج:
قيمة المميز سالبة. اذن، لا يوجد حل للمعادلة. ومنه لا يوجد حل لهذا النظام
عرضنا في الامثلة السابقة انظمة لها حلان، او حل واحد، او ليس لها حل. ولكن، هل يوجد نظام مكون من معادلتين تربيعيتين، له ثلاثة حلول، او اربعة؟ ادرس المثال الاتي
مثال
احل نظام المعادلات التربيعية الاتي، ثم اتحقق من صحة الحل:
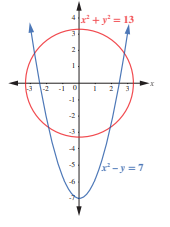
عند تمثيل المعادلتين بيانيا كما في الشكل المجاور، يلاحظ وجود4 نقاط تقاطع بين منحنييهما؛ ما يعني وجود اربعة حلول لنظام المعادلتين. اتحقق من ذلك جبريا.
يظهر المتغير xفي كلتا المعادلتين بالقوة نفسها؛ لذا يمكنني استعمال الحذف للتخلص من هذا المتغير، ثم حل المعادلة التربيعية الناتجة التي تحوي متغيرا واحدا هو y:
يمكنني حل المعادلة التربيعية الناتجة باستعمال القانون العام، او التحليل:
اذن: y=-3,y=2
اعوض قيمتي y في احدى معادلتي النظام لايجاد قيم x:
اذن، x=2,x=-2
اذن، توجد اربعة حلول للنظام، هي:
اتحقق من صحة هذه الحلول بتعويضها في كل من معادلتي النظام