حالات خاصة من متوازي الاضلاع
المستطيل :

هو متوازي اضلاع زواياه الأربع قوائم ، وهذا يعني أن له الخصائص الآتية :
- زواياه الأربع قوائم
- الأضلاع المتقابلة متوازية ومتطابقة
- الزوايا المتقابلة متطابقة
- الزوايا المتحالفة متكاملة
- قطراه ينصف كل منهما الآخر
.....................................................................................................................................................................................................................................................................
قطرا المستطيل :
- نظرية قطري المستطيل :
يكون متوازي الأضلاع مستطيلاً إذا وفقط إذا كان قطراه متطابقين .
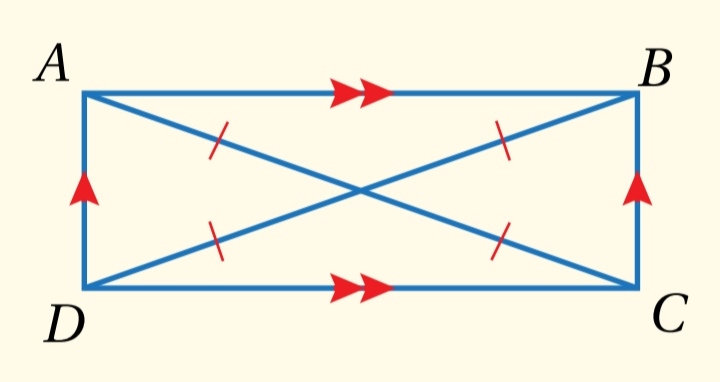
مثال : يكون مستطيلاً إذا وفقط إذا كان
.....................................................................................................................................................................................................................................................................
مثال ( 1 ) :
يبين الشكل المجاور المستطيل ABCD ، أثبت أن قطري المستطيل ABCD متطابقان ، باستعمال البرهان ذي العمودين.
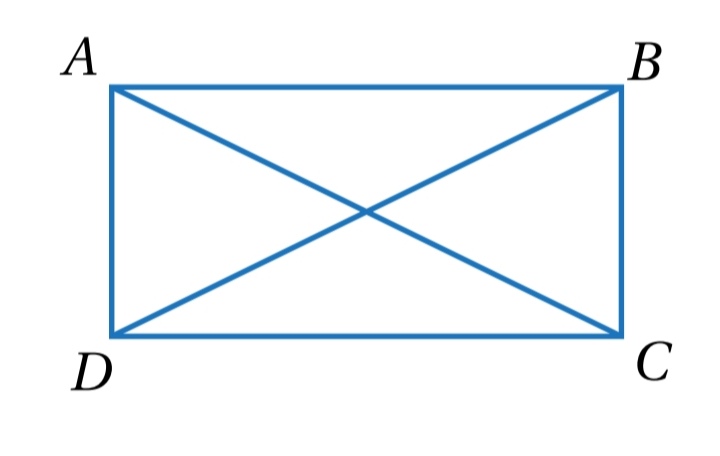
الحل :
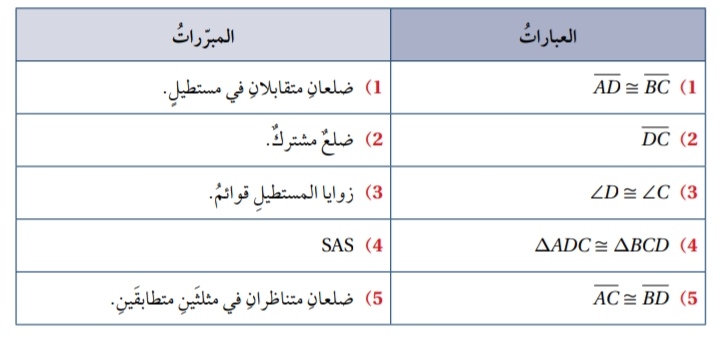
.....................................................................................................................................................................................................................................................................
مثال ( 2 ) :
إذا كان QRST مستطيلاً ، وكان فأجد قيمة المتغير x

الحل :
بما أن QRST مستطيل ، فإن قطريه متطابقان ، إذا أجد قيمة x التي تجعل
.....................................................................................................................................................................................................................................................................
مسألة حياتية :
يبين الشكل المجاور إطار نافذة أبعادها موضحة في الشكل :
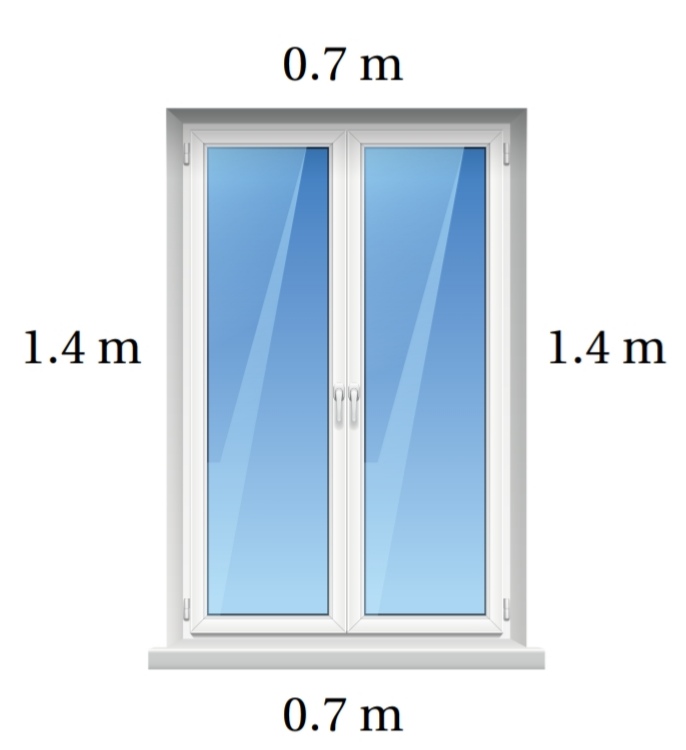
1) هل إطار النافذة على شكل مستطيل ؟ أبرر إجابتي
الحل :
من الشكل نجد أن :
أضلاع الإطار المتقابلة لها الطول نفسه ، إذن الاطار على شكل متوازي أضلاع
ولكن لا يوجد ما يدل على أن الزوايا قوائم ، لذا لا يمكن تحديد ما إذا كان الإطار على شكل مستطيل أم لا
............................................................................................................................................................................................................
2) قاس تميم طولي قطري الإطار ، فوجد أن أحدهما 2.45m وطول الآخر 2.40m ، فهل إطار النافذة على شكل مستطيل ؟ أبرر إجابتي
الحل :
حسب نظرية قطري المستطيل ، يكون الشكل الرباعي مستطيل إذا كان قطراه متطابقين ،
وبما أن قطري إطار النافذة ليسا متطابقين ، إذن فإطار النافذة ليس على شكل مستطيل .
.....................................................................................................................................................................................................................................................................
المعين :
هو متوازي أضلاع أضلاعه جميعها متطابقة
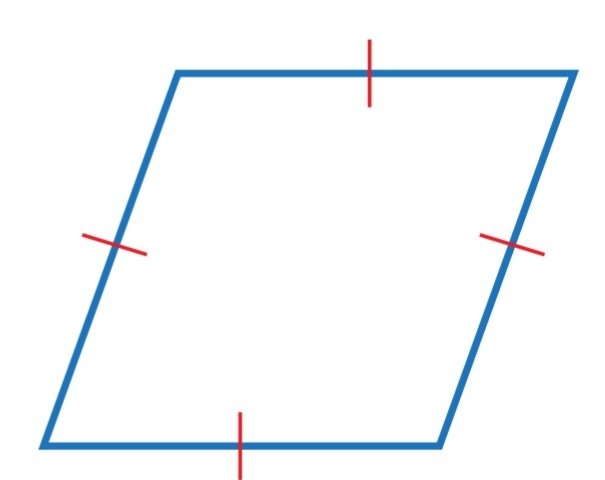
( للمعين خصائص متوازي الأضلاع جميعها ) إضافة إلى الخاصيتين الآتيتين :
- نظرية قطري المعين :
يكون متوازي الأضلاع معيناً إذا وفقط إذا كان قطراه متعامدين .
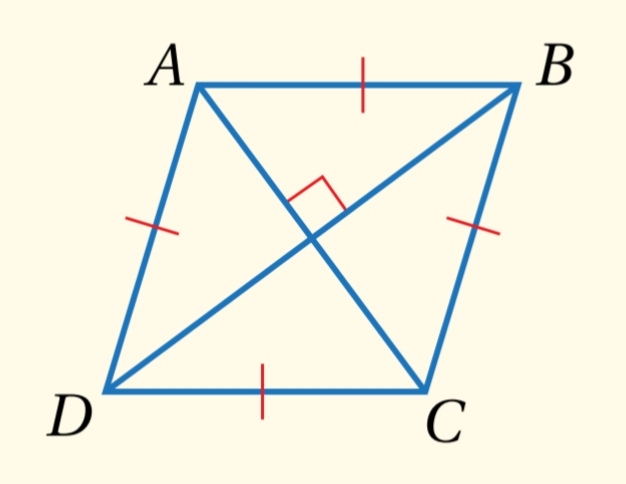
مثال : يكون معيناً إذا وفقط إذا كان
..................................................................................................................................................................................................................
- نظرية الزوايا المتقابلة في المعين :
يكون متوازي الأضلاع معيناً إذا وفقط إذا نصف كل قطر من قطريه الزاويتين المتقابلتين اللتين يصل بين رأسيهما
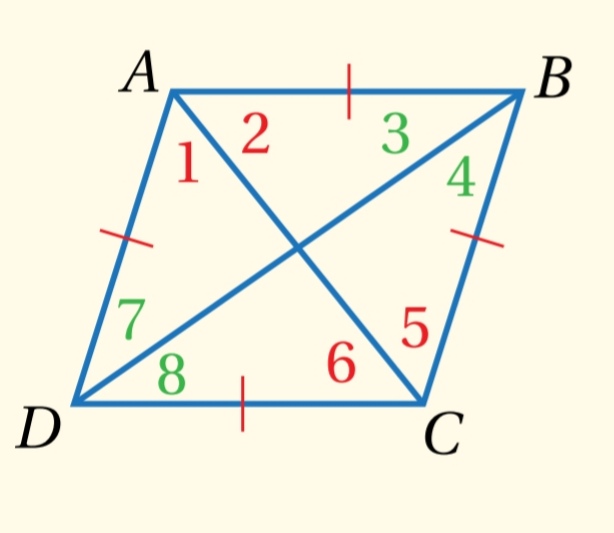
مثال :
يكون معيناً إذا وفقط إذا نصف AC كلاً من ونصف BD كلاً من وهذا يعني أن
.....................................................................................................................................................................................................................................................................
مثال ( 4 ) : يبين الشكل المجاور المعين NPQM ، إذا كانت ، فأجد قياسات الزوايا المرقمة في الشكل.
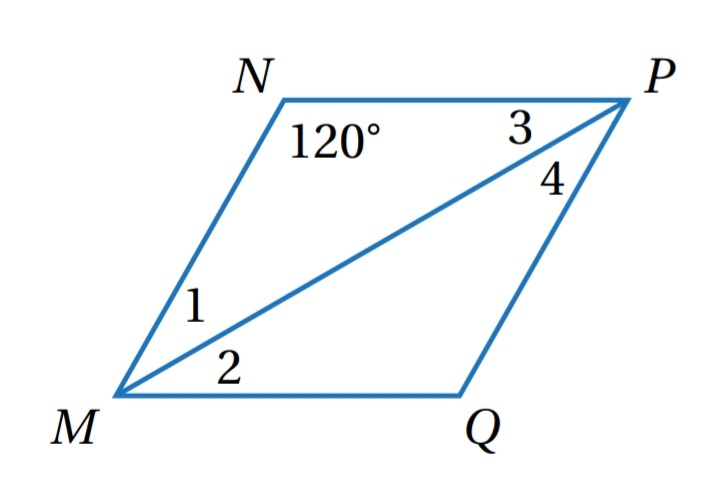
الحل :
ومنه فإن
وبحسب نظرية الزوايا المتقابلة في المعين فإن ، وهذا يعني أن
.....................................................................................................................................................................................................................................................................
المربع :
هو متوازي أضلاع أضلاعه جميعها متطابقة ، وزواياه الأربع قوائم ،
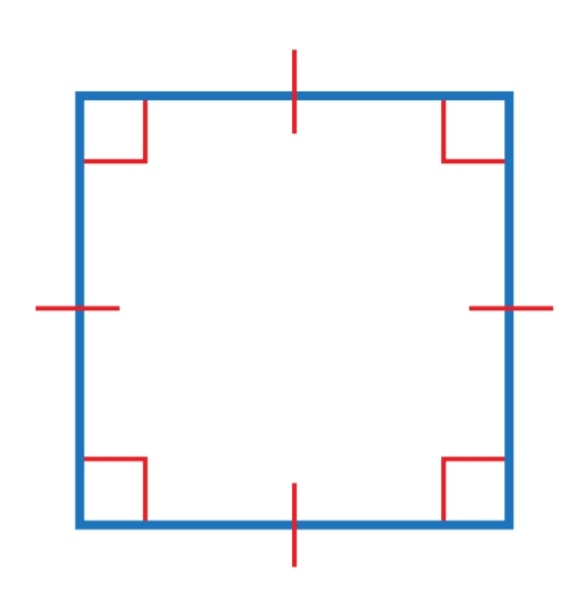
وبما أن المستطيل متوازي أضلاع زواياه الأربع قوائم ، والمعين متوازي أضلاع أضلاعه الأربعة متطابقة ،
فإن المربع مستطيل ، لأن زواياه الأربع قوائم .
وهو أيضاً معين لأن أضلاعه الأربعة متطابقة .
إذن جميع خصائص متوازي الأضلاع والمستطيل والمعين تنطبق على المربع .
.....................................................................................................................................................................................................................................................................
يوضح الشكل الآتي العلاقة بين متوازي الأضلاع والمعين والمستطيل والمربع .
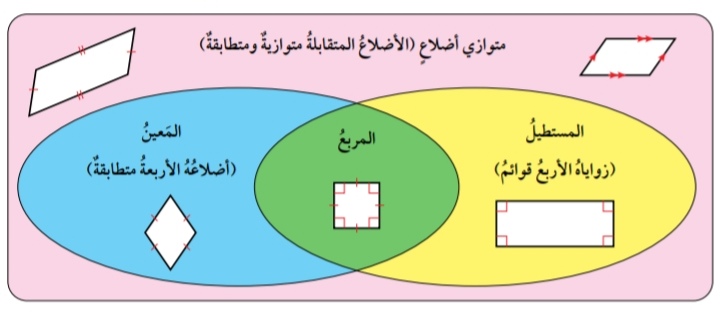
.....................................................................................................................................................................................................................................................................
مثال ( 5 ) :
أحدد ما إذا كان متوازي الأضلاع في كل مما يأتي مستطيلاً أم معيناً أم مربعاً ، مبرراً إجابتي:
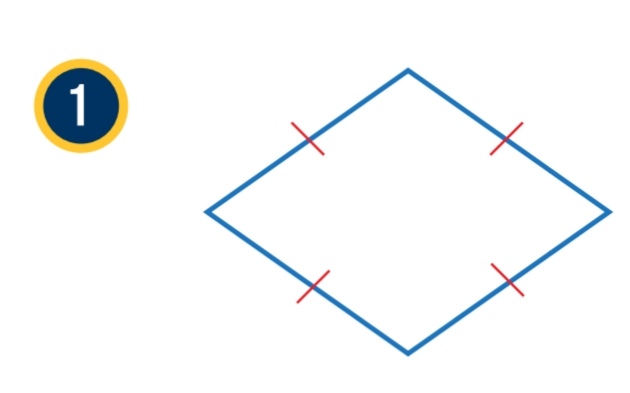
الحل :
بما أن الأضلاع الأربعة لمتوازي الأضلاع المبين في الشكل متطابقة ، فإنه يمثل معيناً
.....................................................................................................................................................................................................................................................................
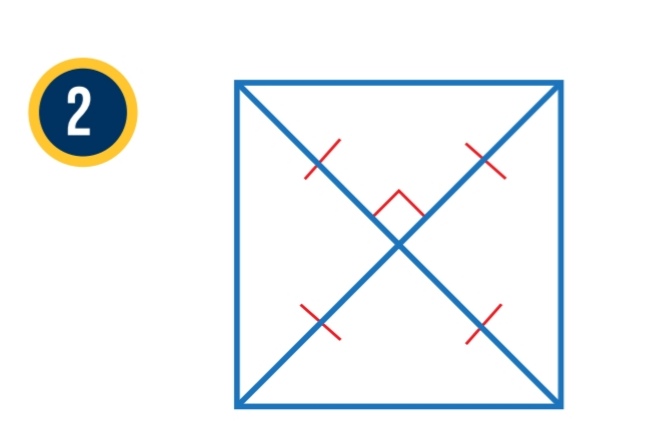
الحل :
بما أن قطري متوازي الأضلاع المبين في الشكل ، متطابقان فإن متوازي الأضلاع مستطيل ، وبما أن القطرين متعامدان،
فإن متوازي الأضلاع معين أيضاً ، ومنه فإن متوازي الأضلاع المبين في الشكل مربع .
.....................................................................................................................................................................................................................................................................