النظامُُ الدوليُُّّ للوحََدات
الفيزياءُ Physics
الفيزياءُ (علمُ الطبيعةِ)، لفظةٌ إغريقيّةٌ تعني معرفةَ الطبيعةِ، وتُعنى بدراسةِ الأنظمةِ بَدءًا منَ الجُسيماتِ المتناهيةِ في الصِّغرِ مثلُ الذَّرةِ إلى المجرّةِ التي تشكّلُ الكرةُ الأرضيّةُ جزءًا بسيطًا منها.يفسّرُ علمُ الفيزياءِ عملَ الكثيرِ منَ الأجهزةِ الكهربائيةِ، والسياراتِ، والطائراتِ، والمَركباتِ الفضائيةِ، والأجهزةِ الطبّيةِ، والخلايا الشمسيةِ، وغيرُها الكثيرُ، وللفيزياءِ مساهمةٌ واضحةٌ في وضعِ أساسياتِ مبادئِ عملِها.
ولعلمِ الفيزياءِ فروعٌ كثيرةٌ ذاتُ أهميّةٍ في عملِ أجزاءٍ مختلفةٍ منَ السيارةِ مثلاً، منها: علمُ الديناميكا الحراريةِ، حيثُ يعتمدُ عليهِ عملُ مُحرّكِ السيارةِ ومُبرِّدِها، وعلمُ الكهرمغناطيسيةِ يعتمدُ عليهِ عملُ البطاريةِ ومصابيحِ السيارةِ، أمّا ضوءُ المصابيحِ وعملُ المرايا فيقعُ ضمنَ علمِ البصرياتِ، أتأمّلُ الشكلَ (1). ويتكاملُ علمُ الفيزياءِ معَ مجالاتِ العلومِ الأخرى كالكيمياءِ، والعلومِ الحياتيةِ، وعلومِ الأرضِ، والرياضياتِ، والهندسةِ، والطبِّ.
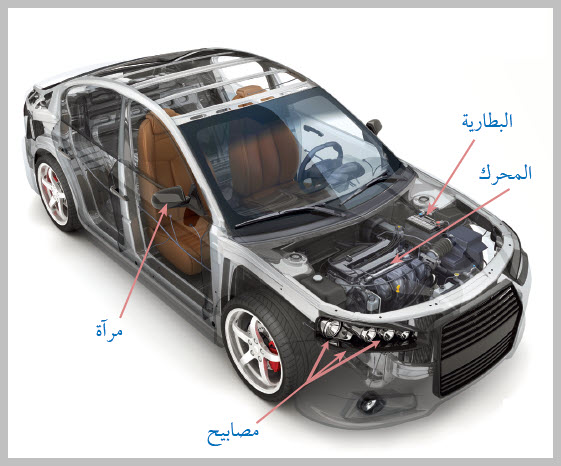
الشكل ( 1): تعتمدُ السيارةُ في عملِها على مجالاتِ الفيزياءِ المختلفةِ.
الكميّةُ الفيزيائيّةُ Physical Quantity
الكتلةُ والطولُ والكثافةُ وغيرُها كلٌّ منها كميّةٌ فيزيائيةٌ Physical Quantity توصَفُ بها الأجسامُ؛ بعضُها قابلٌ للقياسِ بشكلٍ مباشرٍ ؛ الكتلةُ مثلًا، أو غيرِ مباشرِ ؛ مثلُ كثافةِ قطعةٍ فلزيّة. أُعبّرُ عنِ الكميّةِ الفيزيائيّةِ بقيمةٍ عدديّةٍ غالبًا تتبعُها وَحدةُ قياسٍ.فيمكنُني وصفُ مبنًى بأنَّ ارتفاعَه يساويى( 12m )، أو زمنِ اختبارٍ (45min)، أو كتلةِ حجرٍ ( 3kg )وغيرُها الكثيرُ. وألاحظُىأنَّ مقاديرَ هذهِ الكميّاتِ قد أُتبِعتْ بوحَداتِ قياسٍ عُبّر عنها برموزها وهي (kg ،min ،m) على الترتيبِ.

النظامُ الدوليُّ للوحداتِ International System of Units
استخدمَ العربُ الباعَ والذراعَ لقياسِ الطول، في حينِ استخدمَ الرومانُ الميلَ والقدمَ.
وفي القرنِ التاسعَ عشرَ تم تبني النظامِ المتريِّ المعروفِ بنظامِ ( mks ) في أوروبا، حيثُ اعتمدَ وحَداتِ قياسِ المترِ (m) للمسافةِ، والكيلو غرامِ ( kg ) للكتلةِ، والثانيةِ ( s) للزمنِ، ويوجَدُ نظامٌ آخرُ ( cgs ) للقياسِ يعتمدُ الغرامَ ( g) للكتلةِ، والسنتيمترَ (cm) للمسافةِ و ( s) الثانيةَ للزمنِ. ألاحظُ اختلافَ وحَداتِ القياسِ منْ بلدٍ إلى آخرَ، ومنْ زمنٍ إلى آخرَ أيضًا.
في عامِ 1960 اتّخذَ المؤتمرُ الدوليُّ الحادي عشرَ للأوزانِ والمقاييسِ الذي عُقدَ في باريس قرارًا باعتمادِ النظامِ الدوليِّ للوحَداتِ ( SI )، وهذا الاختصارُ جاءَ منَ التسميةِ الفرنسيةِ (Système International) d’Unites حيثُ اتُّفِقَ على اعتمادِ سبعِ كميّاتٍ أساسيةٍ ( Basic Units )،ووحداتِ قياسِها المُبيَّنةِ في الجدولِ (1) وسُمّيَتْ كميّاتٌ أساسيّةٌ؛ لأنَّهُ لا يمكنُ التعبيرُ عنها بدلالةِ كميّاتٍ أساسيّةٍ أخرى.أمّا الكميّاتُ التي يمكنُ التعبيرُ عنها بدلالةِ الكميّاتِ الأساسيّةِ، فيُطلَقُ عليها اسمَ كميّاتٍ مشتقّةٍ (Derived Units )، والجدولُ ( 2) يبيّنُ أمثلةً منها معَ وحَداتِ قياسِها.
قواعدُ التعاملِ معَ وحَداتِ القياسِ
عندَ التعاملِ معَ الوحَداتِ يجبُ أخْذُ الأمورِ الآتيةِ في الحُسبانِ:
1- الوحَداتُ المركّبةُ الناتجةُ عنْ حاصلِ ضربِ وَحْدتينِ أو أكثرَ تُكتب بالترتيبِ نفسِه التي تبدو عليهِ، فمثلاً (newton meter ) تُكتبُ بالترتيبِ نفسِه (N m)
2- الوَحدةُ التي تُضربُ في نفسِها مرةً أو أكثرَ تُكتبُ باستخدامِ الأُسسِ المناسبةِ، فمثلًا (m × m × m =m3)
3- في حالِ قسمةِ الوحَداتِ يُفضَّلُ عدمُ استخدامِ إشارةِ الكسرِ، فمثلًا تُكتبُ (ms-1) أو (m/s)
4- وحَداتُ القياسِ في طرفي المعادلةِ يجبُ أنْ تكونَ متماثلةً، وهذا يُسمَّى التجانسَ، فمثلً لإيجادِ مِساحةِ المستطيلِ (A)، والتي تُعطى بالعلاقةِ: حيثُ طولُ المستطيلِ بوحدةِ المترِ، و ( w) عرضُه بوحدةِ المترِ أيضًا، وبذلكَ فإنَّ الطرفَ الأيمنَ يُقاسُ بوحدةِ ( m × m )، وتمثّلُ مِساحةُ المستطيلِ ووحدةُ قياسِها في النظامِ الدوليِّ للوحَداتِ ( m2 )، وبتعويضِ وحداتِ القياسِ في المعادلةِ أجدُ:
وعلى هذا، فإنَّ المعادلةَ متجانسةٌ.

عندَ جمعِ كميّاتٍ فيزيائيةٍ أو طرحِها، فإنَّ وحَداتِ قياسِ تلكَ الكميّاتِ يجبُ أنْ تكونَ متماثلةً. فمثلًا يمكنُ جمعُ ولكنْ لا يمكنُ جمعُ
لأنَّ وحَداتِ القياسِ مختلفةٌ. وهذا ينطبقُ على طرحِ الكميّاتِ الفيزيائيّةِ أيضًا.
|
أشتقُّ وحدةَ قياسِ حجمٍ متوازي المستطيلاتِ علمًا أنَّ حجمَه ( V) يساوي حاصلَ ضربِ الطولِ ( l ) الحل: أعلمُ أنَّ وَحدةَ قياسِ كلٍّ منَ الطولِ والعرضِ والارتفاعِ هي ( m)، وبتطبيقِ العلاقةِ: |
||
|
يُعبَّرُ عنْ حجمِ الأسطوانةِ بالعلاقةِ: الحلُّ: هي (m2)، فيحينِ وَحدةِ قياسِ ارتفاعِ الأسطوانةِ هي (m). وبالرجوعِ إلى معادلةِ حسابِ حجمِ الأسطوانةِ: (حجمُ الأسطوانةِ)، وعليهِ فإنَّ المعادلةَ متجانسةٌ. |
||
|
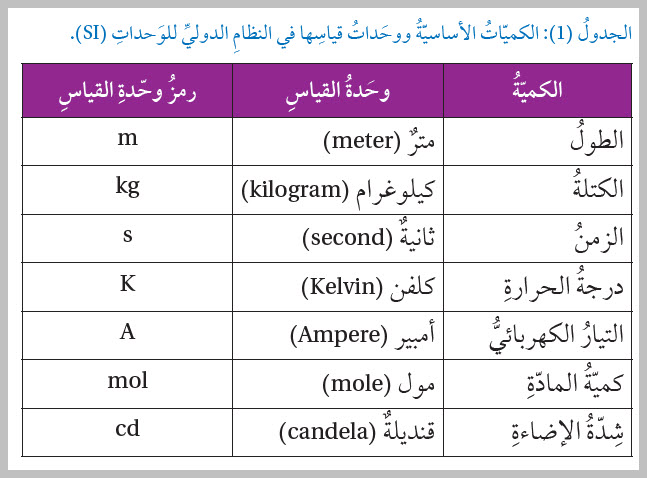
بادِئاتُ النظامِ الدوليِّ للوحَداتِ Unit Prefixes لتسهيلِ التعاملِ معَ الأرقامِ الكبيرةِ جدًّا أو الصغيرةِ جدًّا نستخدمُ البادئاتِ؛ وهي حروفٌ لاتينيةٌ تُكتبُ أمامَ وحدةِ القياسِ على أنْ تدلَّ كلُّ بادئةٍ منها على جزءٍ منْ قيمةِ الكميّةِ الفيزيائيّةِ، أو إحدى مضاعفاتِها منْ قوى العددِ ( 10 ). والجدولُ ( 3) يُظهِرُ بعضَ بادئاتِ الوحَداتِ المعتَمدةِ في النظامِ الدوليِّ للوحَداتِ. فمثلًا المسافةُ بين الشمسِ وأقربِ نجمٍ لها ( 40,000,000,000,000,000) تقريبًا، ولكنْ باستخدامِ البادئاتِ يُكتبُ ( ). الطريقةُ العلميةُ لكتابةِ الأعدادِ Scientific Notation for Writing Numbers ، و( n) عددٌ صحيحٌ موجبٌ أو سالبٌ، فمثلًا:الطولُ الموجيُّ للضوءِ الأحمرِ (700)، ويُكتبُ باستخدامِ الصورةِ العلميّةِ. مُعامِلُ التحويلِ Conversion Factor يمكنُ التحويلُ منْ وَحدةِ قياسٍ إلى أخرى باستخدامِ معاملِ التحويلِ. فعلى سبيلِ المثالِ أعلمُ أنَّ: () تكافئُ ( )، وأستطيعُ استخدامَ ذلكَ لتحويلِ () إلى وحدةِ المترِ على النحوِ الآتي:
ويُسمَّى التعبيرُ () معاملَ تحويلٍ، ويعني أنَّ () تكافئُ ( ).
|
||
|
تمرين أكتبُ الكميّاتِ الآتيةَ بالصورةِ العلميّةِ:
|
||
|
يُقاسُ تردُّدُ الموجاتِ (مثلُ موجاتِ الراديو) باستخدامِ وَحدةِ ( Hz ) وتكافئُ (s-1) أكتبُ ( 500 GHz ) بوَحدةِ ( Hz ) بالصورةِ العلميّةِ. الحلُّ: |
||
|
أكتبُ مقدارَ الطاقةِ () باستخدامِ البادئةِ المناسبةِ. الحل: ( 104 ) أقربُ إلى البادئةِ ( k). وأستخدمُ قواعدَ الأسسِ التي تعلّمْتُها في الرياضياتِ |
||
|
كتلة قَطْرةِ زيتٍ تساوي ( )، أعبّرُ عنْ كتلةِ قطرةِ الزيتِ بوحدةِ () وبالصورةِ العلميّةِ، علمًا أنّ
|
||
|
أجدُ () بوحدةِ (s) حيثُ: الحلُّ: على النحوِ الآتي: |
||
|
سيارةٌ تتحركُ بسرعةِ ()، أجدُ سرعةَ السيارةِ بوحدةِ () الحلُّ:
|
||
|
تمرين
|
||