المجموعاتُ والفتراتُ
Sets and Intervals
فكرةُ الدرسِ : كتابة المجموعات باستعمال طريقتي سرد العناصر والصِّفة المُمَيِّزَة للمجموعة.
التعبيرُ عن المُتباينات باستعمال الفترات.
أولًا : المجموعةُ وطرائقُ التعبيرِ عنها
• المجموعةُ : تجمعُ أشياء مُتَمايِزَةً تحملُ صفةً مشتركةً ، وتسمّى كلٌّ من الأشياء التي تكوِّنُ المجموعةَ عُنصرًا ، ويمكنُ أنْ تكونَ عناصرُ
المجموعة أحرفًا أو أعدادًا أو كلمات. فمثلًا، يُعَدُّ يومُ الاثنين عُنصرًا مِنْ عناصرِ مجموعةِ أيامِ الأُسبوع.
• تُستخدم الأحرفُ الكبيرةُ لتسمية المجموعات ، مثل : … , A, B, C, X, Y ، وتُستخدم الأحرف الصغيرة لتسمية عناصر المجموعة، مثل :
• إذا كان a عنصرًا مِنْ عناصر المجموعة A، فإنَّنا نقولُ إنَّ a ينتمي إلى المجموعةِ A، ونكتب ذلك على الصورةِ: a ∈ A ؛ حيثُ يُستخدم الرمزُ (∋)
للدلالةِ على (ينتمي إلى). ومِنْ ناحيةٍ أُخرى إذا كان b لا ينتمي إلى المجموعة A، فإنَّنا نكتبُ ذلك على الصورة : b ∉ A ؛ حيثُ يُستخدم الرمزُ (∌)
للدلالة على (لا ينتمي إلى).
• يمكنُ التعبيرُ عن المجموعةِ بطريقة سرد العناصر ، بحيث تُكتَب عناصر المجموعة داخل رمز المجموعة { }، وَيُفصَل بين كلِّ عنصر وآخَر بفاصلة.
فمثلًا ، نُعَبِّرُ عَن المجموعة A، التي عناصرُها الأعدادُ الكُليَّة التي تقلُّ عن أو تُساوي 4، بطريقة سرد العناصر على الصورة:
• يمكنُ أيضًا التعبيرُ عَنِ المجموعةِ باستعمالِ الصِّفةِ المُمَيِّزَةِ للمجموعةِ. فمثلًا ، يمكنُ التعبيرُ عَنِ المجموعةِ {4 , 3 , 2 , 1 , A ={0 بطريقةِ
الصفة المميزة { A ={x | x ≤ 4, x ∈ W ، وتُقرأ : مجموعة الأعداد x ؛ حيث ينتمي x إلى مجموعة الأعداد الكُليَّة التي تقلُّ عن أو تُساوي 4.
مثال :
أُعَبِّر عن كلٍّ من المجموعات الآتية مستعملًا طريقة سردِ العناصر، وَطريقة الصِّفة المُميِّزة :
1) مجموعة الأعداد الكُليّة الّتي تقلّ عن أو تساوي 10
الحل :
طريقة سردِ العناصرِ : { 10 , 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 , 0} = A
طريقةُ الصِّفة المُميّزة :
2) مجموعةُ مُضاعفات العدد 3 التي تقلُّ عن 30
الحل :
طريقة سردِ العناصرِ : { 27 , 24 , 21 , 18 , 15 , 12 , 9 , 6 , 3} = B
طريقة الصِّفة المُميّزة :
3) مجموعة حل المعادلة : 3x - 6 = 0
الحل :
أحل المعادلة أولًا :
طريقة سرد العناصر :
طريقة الصِّفة المُميّزة :
ثانيًا : أنواعُ المجموعات
يوجدُ عِدَّة أنواعٍ للمجموعات تبعًا لعدد عناصرها، منها :
• المجموعة الخالية : هي المجموعةُ التي لا تحتوي على أيِّ عنصر ، ويُرمزُ لها بالرَّمز ∅ أو الرَّمز { }، ومن أمثلتها مجموعةُ الأعدادِ الفرديَّةِ التي تقبَل
القِسمة على 2 ، فمن المعلوم أنَّهُ لا يوجد عدد فرديّ يقبَل القسمة على 2 .
• المجموعة المفردة : هِيَ المجموعةُ الَّتي تحتوي على عنصرٍ واحدٍ فقط، وَمِنْ أمثلتِها مجموعةُ حلِّ المُعادلةِ 0 = x + 5 ؛ فَهِيَ تحتوي على عنصرٍ
واحد فقط، هو 5-
• المجموعة المُنتهية : هِيَ المجموعةُ الَّتي تحتوي على عددٍ محدّدٍ منَ العناصرِ، مثلُ { 15 , 12 , 9 , 6 , T = {3 ؛ حيثُ تحتوي على 5 عناصرَ.
• المجموعة غير المُنتهية : هِيَ المجموعةُ الَّتي تحتوي على عددٍ لا نهائيٍّ منَ العناصرِ، مثلُ مجموعة الأعداد الكُليَّة التي تزيد على 20، وهي :
مثال :
أكتبُ كلَّ مجموعةٍ ممّا يأتي بطريقةِ سردِ العناصرِ، ثمَّ أُحَدِّدُ ما إذا كانتْ خاليةً، أمْ مفردةً، أم منتهيةً، أمْ غيرَ منتهيةٍ :
1) A = {x | x > - 2 , x ∈ Z } 2) B = { x | x = 2k + 1 , k ∈ W } 3) C = { x | 4x + 8 = 0}
4) D = { x | x = 4k , k ∈ W , 0 < x < 3} 5) E = { x | x = , k ∈ W , 1 < k < 5}
الحل :
1) A = {x | x > - 2 , x ∈ Z }
تمثِّل A مجموعةَ الأعداد الصَّحيحة التي تزيد على 2 - ، وَتُكتَبُ بطريقةِ سردِ العناصرِ، كما يأتي:
A = { -2, -1, 0 ,1 , …} ، وهي مجموعةُ غير منتهية.
| •• رُموزٌ رياضيَّةٌ : يُرمَزُ لمجموعةِ الأعدادِ الصَّحيحةِ بالرَّمز Z ، وهِي : {… , 2 , 1 , 0 , 1- , 2- , …} |
2) B = { x | x = 2k + 1 , k ∈ W }
الحل :
تمثِّلُ B مجموعة الأعداد الفرديَّة، وتُكتب بطريقة سردِ العناصِر ، كما يأتي :
B = {1 , 3 , 5 , …} ، وهي مجموعة غير منتهية.
| •• أتعلَّمُ : يُستعملُ المقدارُ 2k + 1 للدَّلالةِ على الأعدادِ الفرديَّةِ حيثُ k عددٌ صحيحٌ. فمثلاً، العددُ 7 عددٌ فرديٌّ، ويمكنُ كتابتُهُ على الصورةِ : |
3) C = { x | 4x + 8 = 0}
تمثِّلُ C مجموعةَ حلِّ المُعادلةِ 0 = 4x + 8 ، وَتُكتَبُ بطريقة سرد العناصر، كما يأتي:
C = {-2} ، وهي مجموعة مُفردة.
4) D = { x | x = 4k , k ∈ W , 0 < x < 3}
الحل :
تمثِّلُ D مجموعةَ مُضاعفات العدد 4، التي تقلّ عن 3. وبما أنّهُ لا توجد أعداد تحقِّقُ هذه القاعدة، فالمجموعة D خالية
ويُرمز لها بالرَّمز ∅ أو الرَّمز { }.
5) E = { x | x = , k ∈ W , 1 < k < 6}
الحل :
تمثِّل E مجموعة مُكعبات الأعداد الكلية الواقعة بين 1 و 6 ، وتُكتب بطريقة سرد العناصر، كما يأتي:
E = { 8, 27, 64 ,125} ، وهي مجموعة مُنتهية .
ثالثًا : المُتباينات والصِّفة المُميزة للمجموعة
تعلَّمتُ سابقًا حلَّ المُتباينة الخطيَّة ، وكان من الصَّعب كتابة جميعِ القِيمِ الَّتي تحققُ المُتباينة ؛ لذا لجأتُ إلى تمثيلِ تلك القِيمِ على خطِّ الأعداد،
ولكنَّ استعمال الصِّفةِ المُميِّزة للمجموعة يوفِّر طريقة مُختصرة للتعبير عن مجموعة حلِّ المُتباينة.
مثال :
أكتبُ مجموعةَ حلِّ كلِّ مُتباينة ممّا يأتي باستعمال الصِّفة المُميِّزة :
1) 4x - 12 20
الحل :
| المُتباينة الأصليَّة | |
| بجمع 12 لطرفي المتباينة | |
| بِقِسمة طرفَي المُتباينة على 4 | |
| بالتبسيط |
إذن ، مجموعة الحل هي
الحل :
| المُتباينة الأصليَّة | |
| بِجمع 7 لِطرفَيِ المُتباينة | |
| بطرحِ 7x مِن طرفَيِ المُتباينة | |
| بِقسمة طرفَي المُتباينة على 2 - ، وتغيير اتّجاه رمز المتباينة | |
| بالتبسيط |
إذن ، مجموعة الحل هي
رابعَا : المُتباينات والفترات
تعلَّمتُ في المثالِ السابقِ كتابةَ مجموعة حلِّ المُتباينة باستعمال الصِّفةِ المُمَيِّزَةِ للمجموعةِ، ويمكنُ أيضًا استعمالُ رمزِ الفترةِ
لكتابةِ مجموعةِ حلِّ المُتباينةِ.
يُستعمَلُ رمزا المالانهاية ( infinity ) أدناهُ للدَّلالةِ على أنَّ الفترةَ غيرُ محُدودة في الاتِّجاهِ الموجب أو السالب.
|
يُقرَأُ الرَّمزُ : المالانهاية الموجبة، وَيُستعمَلُ |
يُقرَأُ الرَّمزُ : المالانهاية السالبة، وَيُستعمَلُ للدَّلالةِ على أنَّ الفترةَ غيرُ محُدودةٍ في الاتِّجاهِ السالبِ. |
يُستعملُ الرَّمزُ ] أو الرَّمزُ [عندما يكون رمزُ المُتباينة ≤ أو ≥ للدَّلالة على انتماء طرف الفترة إليها، وَيُستعمَلُ الرَّمز ) أو الرَّمز ( عندما يكونُ رمزُ
المُتباينة < أو > للدَّلالة على عدم انتماء طرف الفترة إليها.
مفهومٌ أساسيٌّ (الفتراتُ غيرُ المحدودةِ)
إذا كان a وَ b عددَين حقيقيَّين فيمكن التعبير عن كلٍّ من المُتباينات الآتية باستعمال فترة غير محُدودة :
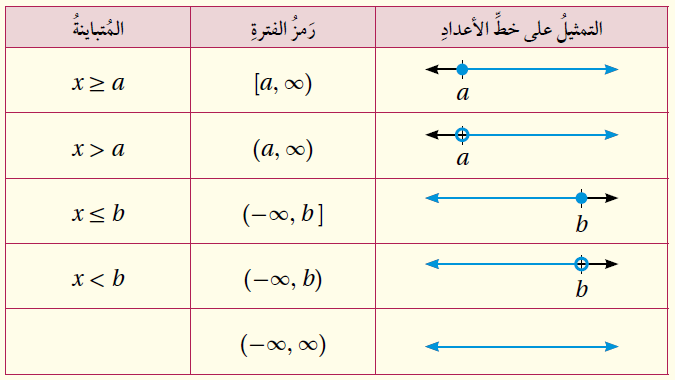
•• أتعلَّمُ : يُستعمَلُ الرَّمزُ ) أوِ الرَّمزُ ( دائمًا معَ المالانهايةِ إذْ إنَّ المالانهايةِ ليستْ عددًا ولا يمكنُ احتواؤها في فترةٍ.
مثال :
أكتب كلَّ مُتباينة ممّا يأتي باستعمالِ رمزِ الفترة، ثمَّ أُمَثِّلُها على خطِّ الأعداد :
1) x < 2 2) x ≥ 4 3) x > -3
الحل :
1) x < 2
رمز الفترة :
التمثيل على خطِّ الأعداد :

2) x ≥ 4
الحل :
رمز الفترة :
التمثيل على خطِّ الأعداد :
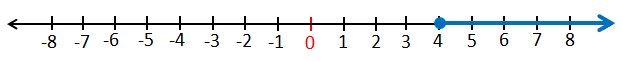
3) x > -3
الحل :
رمزُ الفترة :
التمثيل على خطِّ الأعداد :
