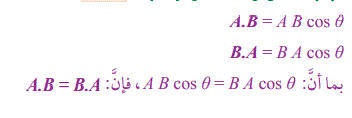الكميات الفيزيائية القياسية والمتجهة
|
الكميات الفيزيائية Physicl Quantity تقسم الكميات الفيزيائية (وهي الكميات القابلة للقياس ) إلى كميات فيزيائية اساسية وكميات أخرى مشتقة، وبعض هذه الكميات يمكن وصفها بشكل كامل عن طريق تحديد مقدارها فقط واخرى عن طريق تحد المقدار والاتجاه معاً. وبوجه عام تقسم الكميات الفيزيائية إلى قسمين رئيسين هما: الكميات القياسية: هي كميات تحدد بمقدار فقط وليس لها اتجاه.فمثلا نقول درجة الحرارة في عمان 9 نهارا دون الحاجة لتحديد اتجاه ، ومن الأمثلة الأخرى على الكميات القياسية : الكتلة، والزمن، والطاقة . الكميات المتجهة: كميات تحدد بمقدار واتجاه معا. فمثلا لا نكتفي بأن نقول أن سرعة الرياح في عمان نهارا 14Km\h وإنما يجب تحديد اتجاهها شرقا. ومن الأمثلة على الكميات المتجهة: الإزاحة والتسارع والقوة. |
 |
مثال 1:
أُصنِّفُ الكمياتِ الفيزيائيةَ في الجدولِ الآتي إلى كمياتٍ
مُتَّجِهةٍ، وأُخرى قياسيةٍ
| الكميةُ الفيزيائيةُ | كميةٌ مُتَّجِهةٌ/ كميةٌ قياسيةٌ |
| الكتلةُ ( 4kg ) | |
| التسارُعُ ( 20m/s2 ) | |
| الشغلُ ( 200J ) | |
| القُوَّةُ ) 120N ، شمالً | |
| الزمن ( 45min) |
الحلُّ:
•الكتلةُ: كميةٌ قياسيةٌ؛ لأنَّها حُدِّدَتْ فقطْ بمقدارٍ.
•التسارُعُ: كميةٌ مُتَّجِهةٌ؛ لأنَّها حُدِّدَتْ بمقدارٍ واتجاهٍ.
•الشغلُ: كميةٌ قياسيةٌ؛ لأنَّها حُدِّدَتْ فقطْ بمقدارٍ.
•القُوَّةُ: كميةٌ مُتَّجِهةٌ؛ لأنَّها حُدِّدَتْ بمقدارٍ واتجاه.
.الزمن: كميةٌ قياسيةٌ؛ لأنَّها حُدِّدَتْ فقطْ بمقدارٍ.
ولكي نميز الكمية المتجهة عن الكمية القياسية كتابةً
يمكننا أن نستخدم إحدى الطريقتين التاليتين :
1- نضع سهم فوق رمز الكمية المتجهة مثل للتعبير عن متجه القوة
2- كتابة رمز الكمية المتجهة بخط غامق مثل F للتعبير عن متجه القوة.
أما إذا أردنا التعبير عن مقدار المتجه فقط دون اتجاه فيمكن وضع الرمز
بين إشارتي القيمة المطلقة أو كتابة الرمز بخط عادي دون سهم فمثلا
نعبر عن مقدار القوة على النحو التالي: أو
|
مثال 2: أُجيبُ بـ (نعمْ) أوْ (لا)، مُعزِّزًا إجابتي بمثالٍ على كلٍّ ممّا يأتي: هلْ يُمكِنُ أنْ تكونَ الكميةُ القياسيةُ سالبةً؟
الحلُّ: والإشارةُ السالبةُ هنا لا تعني اتجاهًا. الخطُّ المستقيمُ منْ نقطةِ البدايةِ إلى نقطةِ النهايةِ( كميةٌ مُتَّجِهةٌ، ووحدةُ قياسِ كلٍّ منْ هاتيْنِ الكميتيْنِ هيَ نفسُها (المترُ في النظامِ الدوليِّ).
في الجسمِ قُوَّتانِ متساويتانِ في المقدارِ؛ إحداهُما باتجاهِ الشرقِ، والأُخرى باتجاهِ الشمالِ. وقدْ تكونُ هذهِ الكمياتُ مختلفةً |
|
تمرين صفحة ( 12). في أثناءِ جلوسي في غرفةِ الصفِّ سقطَ قلمٌ باتجاهِ سطحِ الأرضِ. أُحدِّدُ كميتيْنِ قياسيتيْنِ وكميتيْنِ مُتَّجِهتيْنِ لها صلةٌ بذلكَ. الجواب: كميتان قياسيتان: كتلة القلم ، الزمن اللازم لوصول القلم إلى سطح الأرض. كميتان متجهتان: سرعته المتجهة ، وزن القلم (تسارع السقوط الحر ). |
|
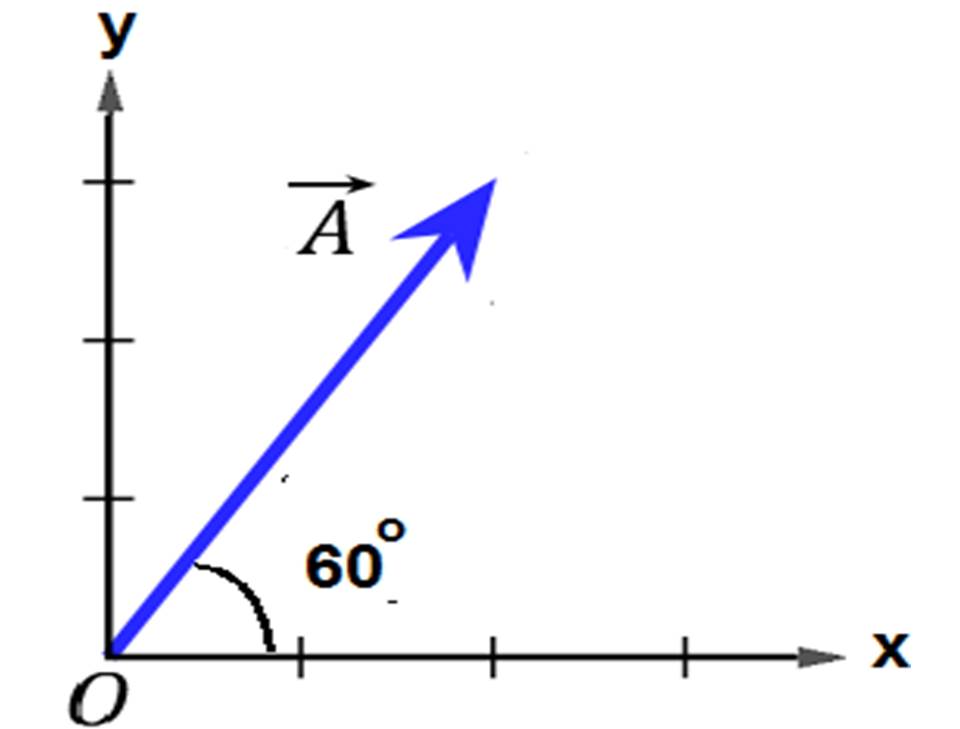
تمثيل المتجهات بيانيا: لتمثيل الكمية المتجهة بيانيا نتبع التالي: - نرسم مستوى احداثيا (x-y)، ونقطة إسناد مثل نقطة الأصل (0-0) - نرسم سهما يقع ذيله( نقطة البداية) عند نقطة الأصل بحيث يمثل طول السهم مقدار المتجه. - يحدد اتجاه السهم إما باستخدام الاتجاهات الجغرافية ( شمال ، جنوب، شرق، غرب) ، وإما باستخدام الزاوية المرجعية وهي الزاوية التي يصنعها المتجه مع محور (x+) بعكس دوران عقارب الساعة . في الشكل المقابل الزاوية ( ) والتي تساوي 60o تسمى الزاوية المرجعية، ويعبر عن المتجه ( A ) بصيغة رياضية كما يلي:
|
 |
|
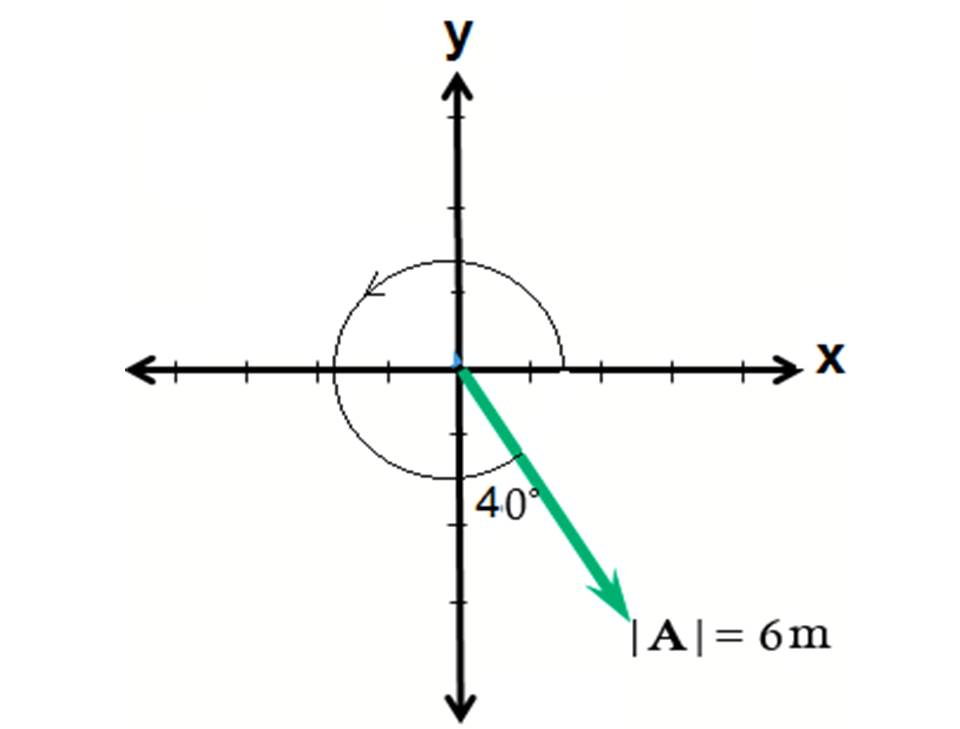
مثال :3 مثل الكمية المتجهة في الشكل المقابل بالصيغة الرياضية الجواب: بتطبيق الصورة العامة للمتجه:
مقدار المتجه: الزاوية المرجعية: إذا التمثيل الرياضي المتجه كما يلي: |
 |
|
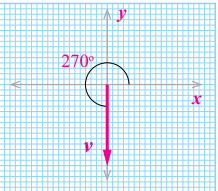
مثال4: اكتسب جسم متجه سرعة ( ) . مثل متجه السرعة بيانيا. الحل:
فيكون طول السهم (3cm = 3×1 )
الأصل( 0,0 ) ويصنع زاوية 2700 مع المحور (+x) عكس عقارب الساعة( الجنوب) |
 |
|
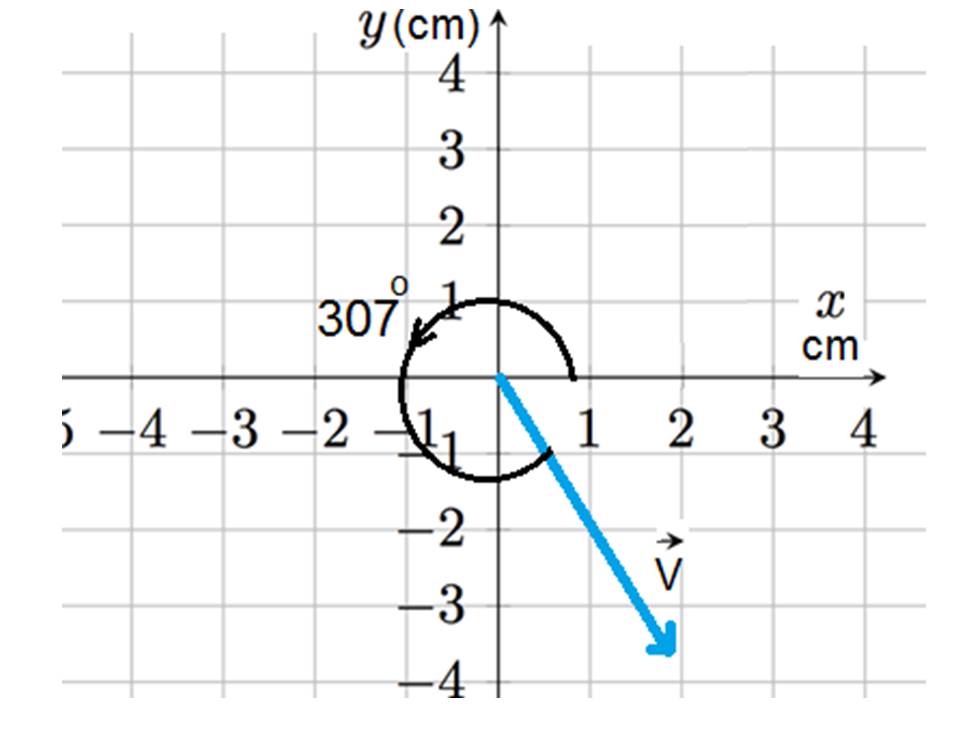
تمرين صفحة 14 تسيرُ سيارةٌ بسرعةٍ v مقدارُها 80km/h ، في اتجاهٍ يَصنعُ زاويةً مقدارُها 37o جنوبَ الشرقِ. أُمثِّلُ مُتَّجِهَ السرعةِ بيانيًّا.
الحل: نستخدم مقياس رسم مناسب،ليكن: 1cm يمثل 20N، لذلك طول السهم 4cm، ثم نرسم سهم طول 4cm `ذيله عند نقطة الأصل ويصنع زاوية ( 37o ) جنوب الشرق ( في الربع الرابع ) أي يصنع زاوية ( 307o ) مع محور السينات ( +x ) بعكس دوران الساعة. كما في الرسم البياني التالي: |
|
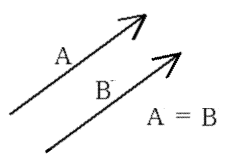
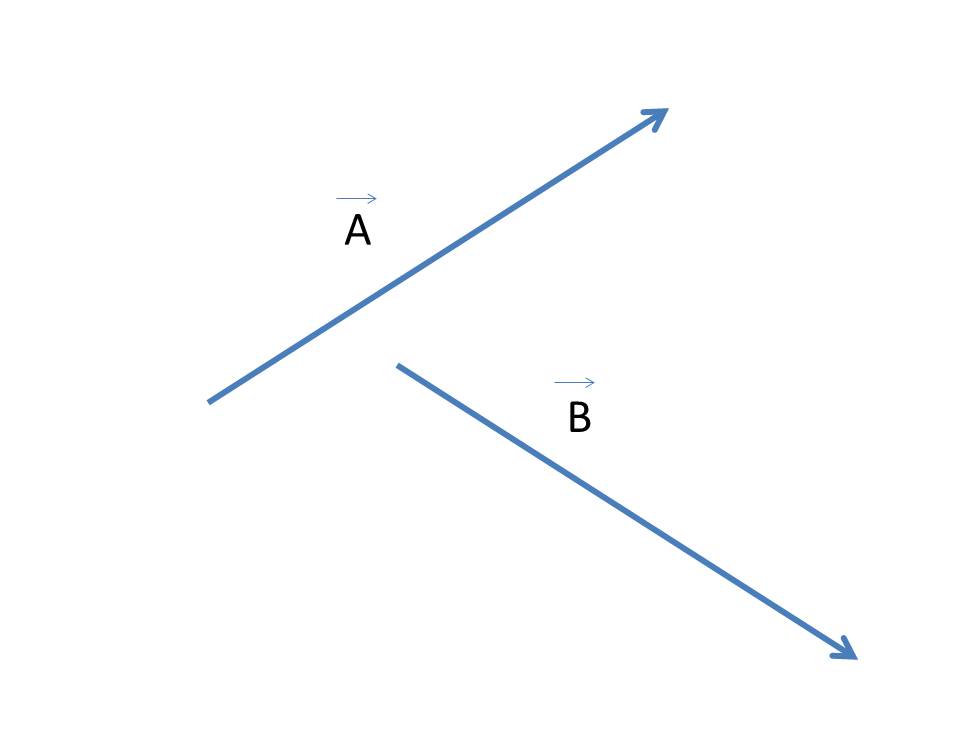
خصائص المتجهات: 1- تساوي المتجهان يتساوى المتجهان عندما يكونان من نفس النوع ولهما نفس المقدار والاتجاه. كما في الشكل ( أ )المقابل: ويعبر عنهما كما يلي: بينما إذا اختلف المتجهان في المقدار أو الاتجاه أو كليهما معاً فإنهما غير متساويان فالمتجهان ( A ) , (B ) الشكل ( ب ) المقابل، متساويان في المقدار ومختلفان في الاتجاه، لذلك يعتبران متجهان غير متساويان، ويعبر عن ذلك كما يلي: |
الشكل (ب): متجهان غير متساويان (متساويان مقداراً ومختلفان في الاتجاه). |
|
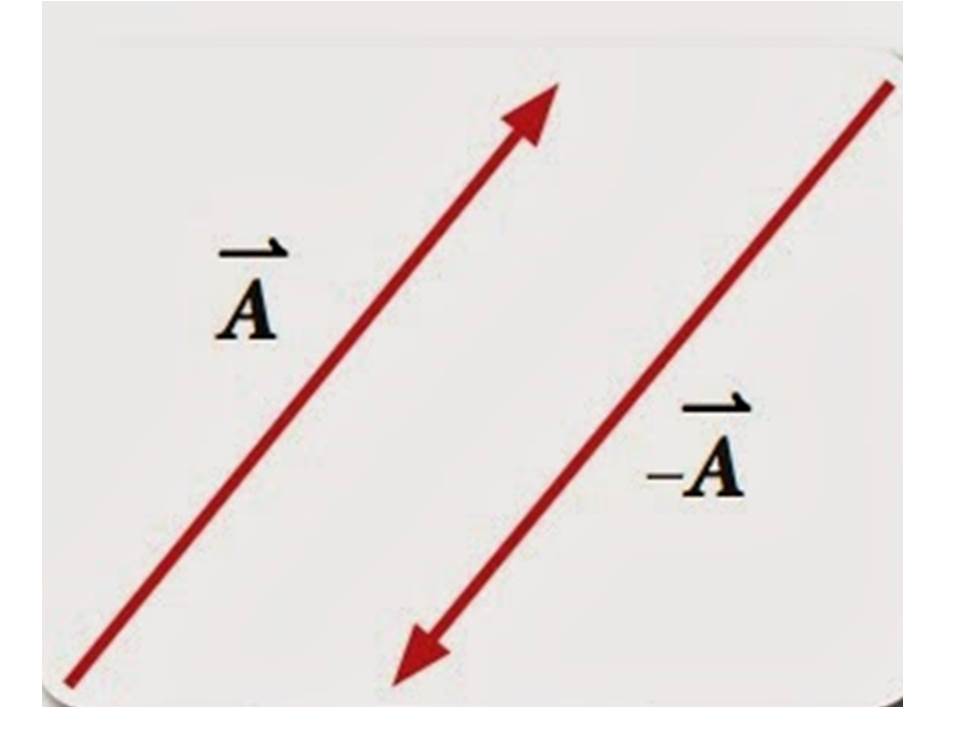
2- سالب( معكوس) المتجه هو متجه له مقدار المتجه الأصلي نفسه ولكنه يعاكسه بالاتجاه بحيث تكون الزاوية بين المتجه ومعكوسه 180o. |
 |
|
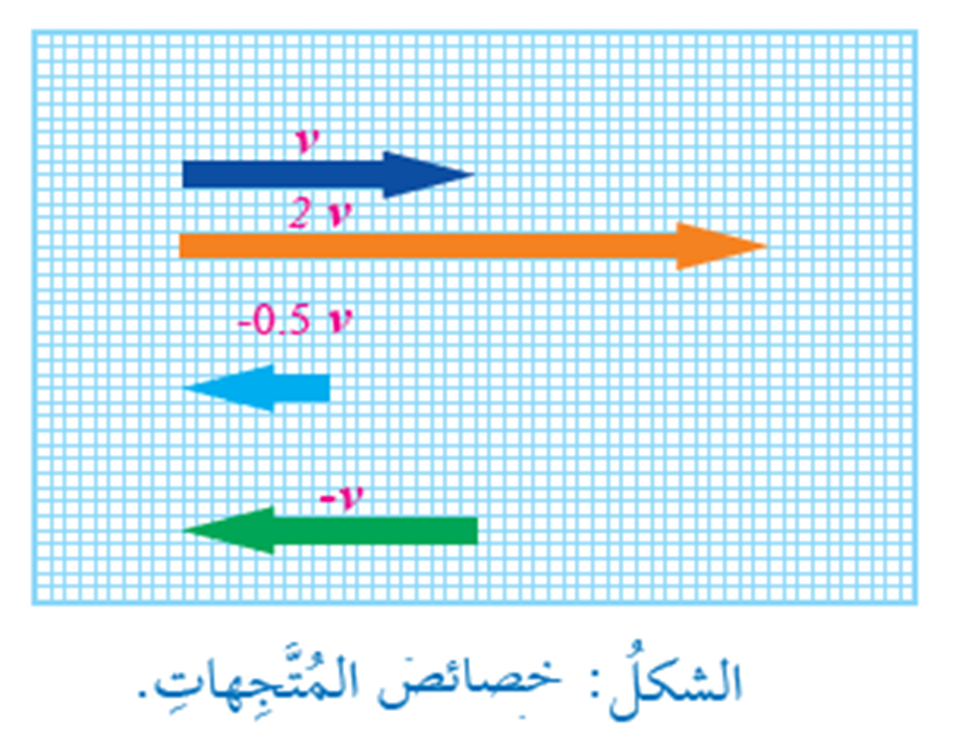
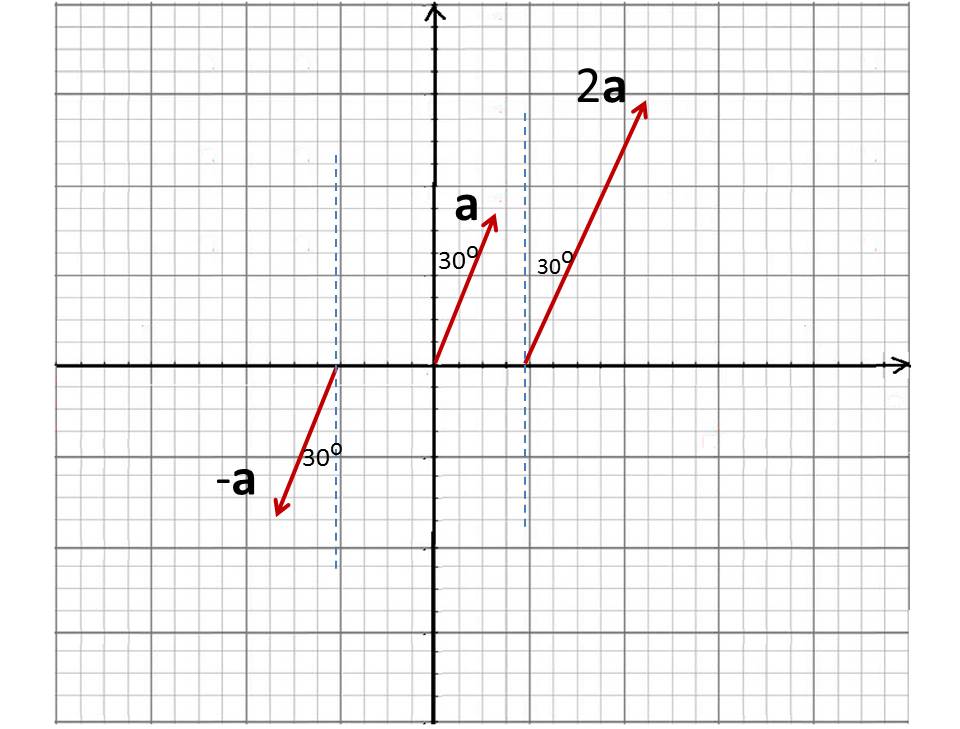
3-ضرب المتجه في كمية قياسية عند ضرب متجه مثل () بكمية قياسية (عدد حقيقي(n) نحصل على متجه جديد ( n) يعتمد اتجاهه على اشارة n
يكون بنفس اتجاه المتجه
يكون عكس اتجاه المتجه c
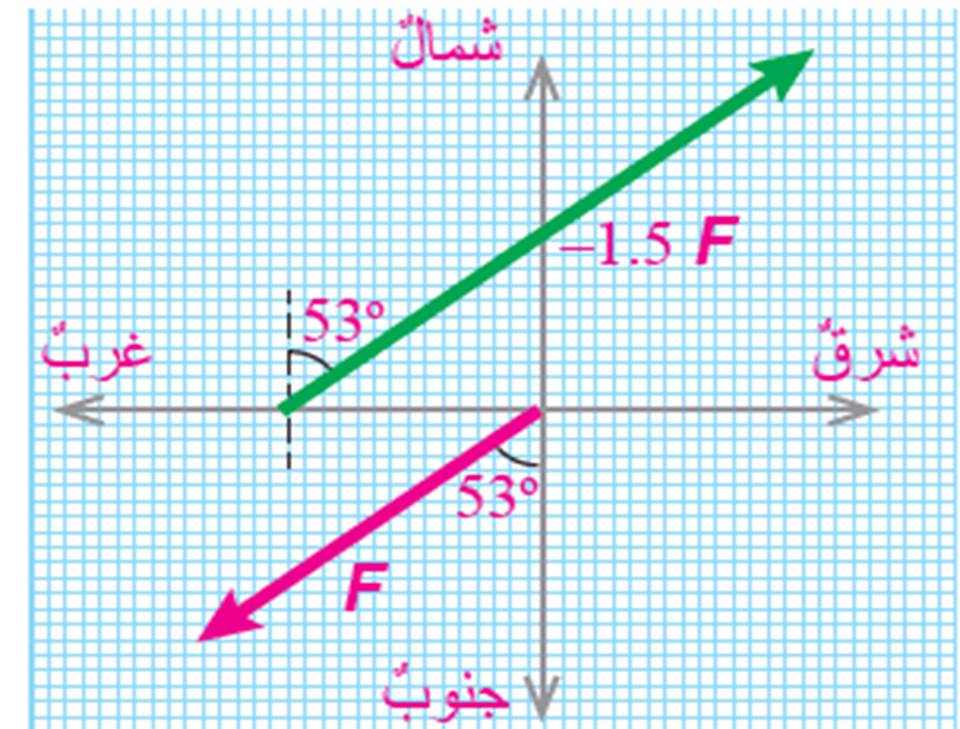
حسب قانون نيوتن الثاني ، يكون متجه القوة المحصلة ( ) ناتج حاصل ضرب الكتلة ( m ) في متجه التسارع ( ) أي أن: وبما أن الكتلة ( m ) دائما موجبة فان القوة المحصلة والتسارع يكونان في الاتجاه نفسه . مثال 5: تتحرَّكُ عربةٌ بسرعةٍ مُتَّجِهةٍ v مقدارُها 40m/sفي اتجاهِ الشرقِ. أُمثِّلُ بيانيًّا: الحلُّ: ليُمثِّلَ المُتَّجِهَ ( v) باتجاهِ الشرقِ، كما في الشكلِ المقابل . مثال 6 تُؤثِّرُ قُوَّةٌ F مقدارُها 250N في جسمٍ باتجاهٍ يَصنعُ زاويةً مقدارُها 53o غربَ الجنوبِ. أُمثِّلُ بيانيًّا: أ . مُتَّجِهَ القُوَّةِ .F ب . المُتَّجِهَ ( 1.5 F –). الحلُّ: أ . أختارُ مقياسَ الرسمِ ( 1cm : 50 N )، ثمَّ أرسمُ سهمًا طولُهُ 5 cm ليُمثِّلَ المُتَّجِهَ F، كما في الشكلِ المقابل . واتجاهُهُ معاكسٌ لاتجاهِ F؛ أيْ بزاويةٍ مقدارُها 53o شرقَ الشمالِ )أوْ بزاويةٍ مقدارُها 37o شمالَ الشرقِ ، كما في الشكلِ. |
|
|
تمرين صفحة 16 تسيرُ سيارةٌ بتسارعٍ ثابتٍ a = 3 m/s2 في اتجاهٍ يَصنعُ زاويةً مقدارُها 30o شرقَ الشمالِ. أُمثِّلُ بيانيًّا أ. سالبَ المُتَّجِهِ a . ب. ضربَ المُتَّجِهِ a في العددِ (2). الحل: (مقياس الرسم (1cm :1 m/s2)، إذن، طول السهم الذي يُمثِّل المتجه a هو 3cm كما في الشكل. وطول المتجه ( 2a ) هو 6cm.) أ- سالب المتجه هو ( a - ) ويصنع زاوية 1800 معه، أي أن : . مع محور السينات الموجب بعكس دوران الساعة أو ( 30o ) غرب الجنوب ب- 2a هو متجه طوله وبنفس اتجاه a أي (30o) شرق الشمال |
|
ضرب المتجهات:
بالاضافة الى ضرب المتجهات بقيمة قياسية فاننا نحتاج لضرب كمية
متجهة في اخرى لايجاد كمية جديدة قد تكون قياسية او متجهة .
فيوجد نوعان لضرب المتجهات هما : الضرب القياسي والضرب المتجهي.
1- الضرب القياسي( النقطي)
هو ضرب متجهين مثل (A,B)بحيث يكون الناتج كمية قياسية لها مقدار فقط
حسب العلاقة:
حيث Aمقدار المتجه الأول
B: مقدار المتجه الثاني
:الزاوية الصغرى بين المتجهين
|
قارن بين A.Bو B.A
|
 |
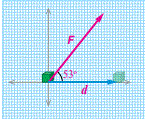
من التطبيقات الفيزيائية على الضرب القياسي الشغل Wوهو حاصل
الضرب القياسي للقوةF في متجه الازاحةd:
|
مثال7: أثرت قوة F مقدارها ( 120N) في جسم فحركته ازاحة d=5m في اتجاه الشرق ، اذا علمت أن الشغل يعطى بالعلاقة وأن الزاوية بين القوة والازاحة ، فاجيب عما يأتي: أ- أمثل المتجهين F و d بيانيا. ب- هل يعد الشغل كمية متجهة ؟ اوضح ذلك ج- أجد مقدار الشغل الذي انجزته القوة. الحل: ب- لا . لايعد الشغل كمية متجهة بل قياسية لانه ناتج عن الضرب القياسي لمتجهي القوة والازاحة ج-
|
 |
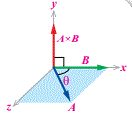
ب- الضرب المتجهي( التقاطعي)
هو ضرب متجهين مثل (A,B) بينهما زاوية يكتب في صورة (A x B) بحيث يكون الناتج كمية
متجهة لها مقدار واتجاه عمودي على كل من اتجاهي المتجهين.
|
ويعطى الضرب المتجهين بالعلاقة:
حيث: A: مقدار المتجه الأول B: مقدار المتجه الثاني : الزاوية الصغرى بين المتجهين |
 |
|
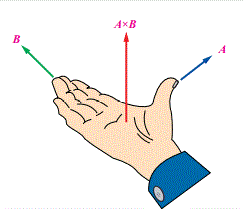
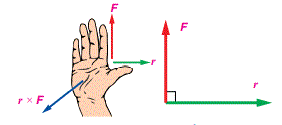
لتحديد اتجاه ناتج الضرب المتجهي نستخدم قاعدة اليد اليمني حيث يشير الابهام الى اتجاه المتجه الأول (A) ، وتشير الأصابع الى متجه الثاني(B) فيكون الناتج (AxB) متجه عمودي وخارج من الكف. |
 |
|
المثال 8: في الشكل (14) اذاكان F=250N , r= 0.4m . فأجيب عما يأتي: أ- أجد مقدار عزم القوة (rxF) واتجاهه. ب- اذا تغيرت الزاوية بين r و لتصبح 1350 ، فما مقدار () واتجاهه. الحل: أ . مقدارُ عزمِ القُوَّةِ : r × F الأصابعُ إلى اتجاهِ F ؛ لذا يكونُ اتجاهُ عزمِ القُوَّةِ خارجًا منَ الورقةِ (باتجاهِ محورِ . +z ) ب . مقدارُ :r × F
اتجاهُ r × F يكونُ خارجًا منَ الورقةِ (باتجاهِ محورِ z+)، كما في الفرعِ الاسبق ( أ ) |
 |
تمرين صفحة 20
متجهان A و B مقدار كل منهما 20u أجد مقدار الزاوية بين المتجهين
في الحالتين الاتيتين:
أ-
ب-
الحل:
أ.
ب.
مثال 9
إذا كان مقدار( = 2 u A ) ومقدار ( = 3u B)، أوجد مقدار ( A x B ) محدداً اتجاهه لكل
من الأشكال التالية.
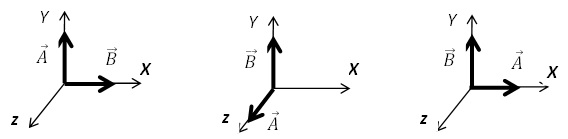
الحل:
مثال 10
متجهان A =3u,60o و B = 2u,113o ، أوجد كل من:
أ. | AxB| ب. A.B
الحل
الزاوية المحصورة بين المتجهين
أ.
ب.