احتمالات الحوادث المستقلة والحوادث غير المستقلة
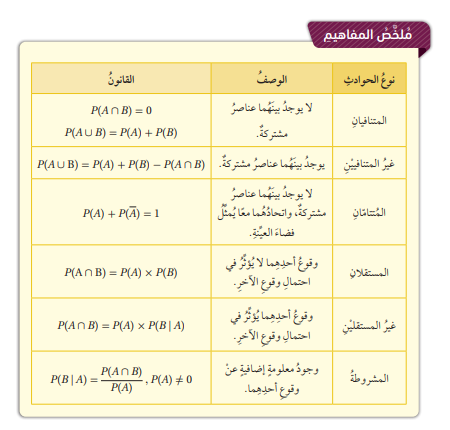
- لأي تجربة عشوائية ، يكون الحادثان A و B مستقلين إذا كان وقوع أحدهما ( أو عدم وقوعه) لا يؤثر في احتمال وقوع ( أو عدم وقوع ) الآخر.
مفهوم أساسي
- بالكلمات : إذا كان A و B حادثين مستقلين في تجربة عشوائية ، فإن احتمال وقوعهما معًا هو حاصل ضرب احتمال وقوع كل منهما .
- بالرموز : إذا كان A و B حادثين مستقلين ، فإن :
مثال
في تجربة إلقاء حجر نرد وقطعة نقد منتظمين عشوائيًا معًا مرة واحدة ، أجد احتمال ظهور العدد 6 على حجر النرد والصورة على قطعة النقد .
أفترض أن A هو حادث ظهور العدد 6 على حجر النرد
و B هو حادث ظهور الصورة على قطعة النقد
نلاحظ أن وقوع الحادث A أو عدم وقوعه لا يؤثر في وقوع الحادث B أو عدم وقوعه
إذا A و B حادثان مستقلان و إن :
- لأي تجربة عشوائية ، يكون الحادثان A و B غير مستقلين إذا أثر وقوع أحدهما في احتمال وقوع الآخر.
مثال
أحدد إذا كان الحادثان مستقلان أم لا في الحالات الآتية :
1. سحب كرتين على التوالي عشوائيًا من كيس فيه كرات متماثلة مختلفة الألوان ، علمًا بأن سحب الكرة الثانية كان بعد إرجاع الكرة الأولى إلى الكيس .
إرجاع الكرة المسحوبة أولًا إلى الكيس يعني أنه يمكن إعادة سحبها ، أو سحب غيرها ، فتكون فرص سحبها وغيرها من الكرات متكافئة ؛ أي أن نتيجة سحبها لا تؤثر في نتيجة سحب أي كرة أخرى ؛ فالحادثان مستقلان .
2. سحب كرتين على التوالي عشوائيًا من كيس فيه كرات متماثلة ، وعدم إرجاع أي منهما إلى الكيس .
عدم إرجاع الكرة المسحوبة أولا إلى الكيس يعني نقص عدد الكرات المتبقية فيه ، وهذا يعني أن احتمال سحب الكرة الثانية سيتأثر بنتيجة الكرة المسحوبة أولا ؛ فالحادثان غير مستقلين .
3. سحب كرة عشوائيًا من كيس فيه كرات متماثلة حمراء وصفراء ، ثم سحب كرة عشوائيًا من كيس آخر فيه كرات متماثلة حمراء وصفراء .
نتيجة سحب الكرة من الكيس الأول لا تؤثر في نتيجة سحب كرة من الكيس الثاني ؛ فالحادثان مستقلان .
يساعد استعمال الشجرة الاحتمالية على حساب احتمالات الحوادث المستقلة وغير المستقلة .
مثال
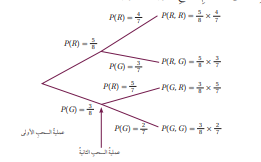
يحتوي كيس على 5 كرات حمراء R و 3 كرات خضراء G جميعها متماثلة . سحبت كرة من الكيس عشوائيًا ، ثم كتب لونها دون إرجاعها إلى الكيس ، ثم سحبت كرة أخرى عشوائيًا ، ثم كتب لونها. أجد احتمال كل من الحوادث التالية باستعمال الشجرة الاحتمالية :
ألاحظ من التمثيل بالشجرة الإحتمالية الآتي كيف تتأثر عملية السحب الثانية بنتيجة عملية السحب الأولى عند عدم إرجاع الكرة المسحوبة :
1. سحب كرتين خضراوين :
2. سحب كرة خضراء في المرة الأولى وكرة حمراء في المرة الثانية
3. سحب كرتين ، إحداهما خضراء ، و الأخرى حمراء
- ألاحظ في المثال السابق أن احتمال سحب كرة خضراء في المرة الأولى وكرة حمراء في المرة الثانية يساوي احتمال سحب كرة خضراء في المرة الأولى مضروبًا في احتمال سحب كرة حمراء ثانية ، علمًا بأن كرة خضراء سحبت في المرة الأولى .
المفهوم الأساسي
- بالكلمات : احتمال وقوع حادثين غير مستقلين يساوي احتمال وقوع الحادث الأول مضروبًا في احتمال وقوع الحادث الثاني بعد وقوع الحادث الأول
- بالرموز : إذا كان A و B حادثين غير مستقلين في تجربة عشوائية ما ، فإن :
- يقرأ الرمز : احتمال وقوع الحادث B شرط وقوع الحادث A ؛ لذا يسمى الإحتمال المشروط ، ويمكن إيجاده باستعمال الصيغة الآتية :
مثال :
ألقي حجر نرد منتظم عشوائيًا مرة واحدة . ما احتمال ظهور العدد 6 إذا كان العدد الظاهر زوجيًا ؟
في هذه التجربة العشوائية ، فضاء العينة هو
إذا كان A هو حادث ظهور العدد 6
و B هو حادث ظهور عدد زوجي ، فإن :
تعني احتمال ظهور العدد 6 إذا كان العدد الظاهر زوجيًا :
- في كثير من الأحيان ، تعرض البيانات لفئتين من الأشياء باستعمال ما يسمى جداول الاتجاهين ، وهي جداول تتيح إيجاد الاحتمال المشروط على نحو سهل .
مثال : من الحياة
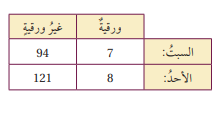
تدوير : يبين الجدول المجاور كتل النفايات التي جمعت بالأطنان في يومين من إحدى المدن . إذا سحبت عينة عشوائية منها قبل البدء بإعادة تدويرها ، فما احتمال أن تكون العينة ورقية ، علما بأنها جمعت يوم الأحد ؟
إذا كان A هو حادث سحبت عينة من الورق ، و B هو حادث سحب عينة أخرى جمعت يوم الأحد ، فما قيمة ؟
الخطوة الأولى :
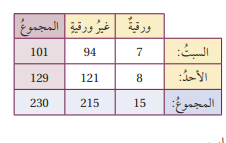
نكمل جدول الاتجاهين بإيجاد المجاميع .
الخطوة الثانية :
نجد احتمالات الحوادث اللزمة لحساب الاحتمال المشروط .
بالنظر إلى جدول الاتجاهين ، أجد كلا من P(A) و P(B) و :
الخطوة الثالثة :
نعوض قيم الاحتمالات بصيغة الاحتمال المشروط .
إذا احتمال أن تكون العينة ورقية وأنها جمعت يوم الأحد هو